円の面積は 半径×半径×π が一般的です。 しかし以下のように考えることもできます。 直径×直径 = (半径×2)× (半径×2) = 半径×半径×4 つまりその後、円を平行四辺形の形に近似的に等積変形し、円の面積の公式を学習する。そ の際、「円周の長さ=直径×3.14」の公式が使われ、 円の面積=半径×半径×3.14 (即ち、円の面積=半径×半径×円周率) であることを知る。楕円の面積 の公式は、次ようになります。 楕円の面積 S=π・a・b 楕円は半径aの円を縦軸方向に b/a倍縮小(拡大)した図形 と考えることができます。 ですから、円の面積公式(π・r・r)の応用と考えると覚えやすいです。
実践記録算数5年
円 面積 公式 直径
円 面積 公式 直径-1)半径で円の面積? みなさんは円の公式を言えますか? 普通科では「πr^2です」とすぐ答えるでしょう。 しかし、工業科では「(πd^2)/4です(四分のパイディーの2乗)」と答えます。 これは、実際に棒の面積を計算するときにすぐ判るはずです。 棒の半径など上手く測れないので、棒の直径を測るはずです。 よって、直径で公式を覚えておくほうが便利です 円の公式 円周・面積 円周率 = 3.14 円周の長さ = 直径 × 円周率 円周率 = 円周 ÷ 直径 おうぎ形の弧の長さ = 直径 × 314 × 中心角 ÷ 360 円の面積 = 半径 × 半径 × 円周率 弧の面積 = 半径 × 半径 × 円周率 × 弧の角度 ÷ 360 円周の長さ 重要 円周率とは、「直径」を何倍したら「円周




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト
たとえば、直径3cmの円があったとすると、円周の長さは、 3 × 314 = 942cm になる。つまり、この円をハサミで切ってあげると、 おおよそ、直径の3倍ぐらいの長さになっているってことだ。 直径と円周率をかけるだけ。 チョー便利な計算公式。実物で玄長・円弧は測れますが誤差が生じるので,また条件により他の公式も併用しています。 <検証> 金属のブロックにひずみゲージを貼付して,荷重を負荷した時のひずみ測定結果と断面積と荷重より求めた応力(ひずみ値)との比較検証・・・応力σ = 荷重P ÷ 断面積A円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 314
円の面積・直径・半径・円周の計算機。公式を使った求め方も 初心者向け半径・直径・円周長・円の面積・球の表面積 円の面積の求め方直径1mの円の面積は?どのようにしてだします 中学数学が秒でわかる!円の面積を直径から求める図付き 円の 円の面積 半径 半径 円周率 円 の 面 積 = 半 径 × 半 径 × 円 周 率 = 4 × 4 × 314 = 5024 c m 2 と求まります。 問②面積が c m 2 の円の円周の長さを求めてください。 (円周率は 314 ) 円の面積の公式から半径を計算したあと 「半径⇒直径⇒円周の 円周の長さを出すために、まず円の直径を知る必要があります。 この円の面積が096㎠であることから 円の面積=半径×半径×314=096(㎠) 半径×半径=096÷314= 64 同じ数をかけて64になるのは8。 半径が8cmとわかったので、直径はその2倍の16cm
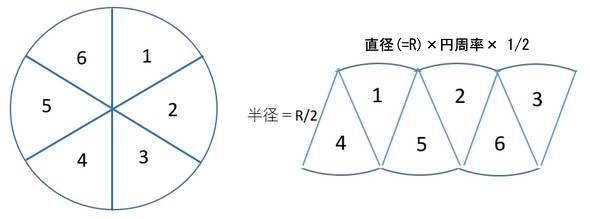
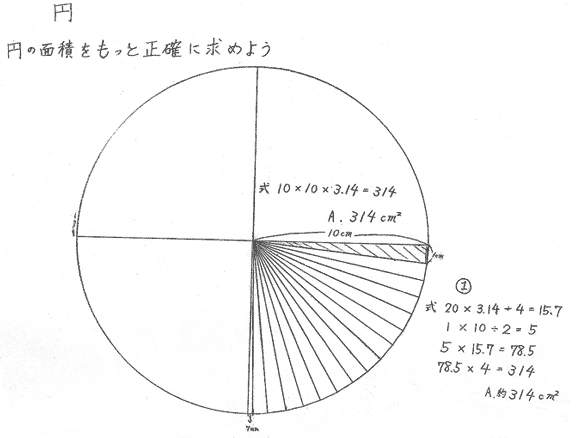
円を扇形に切って並べ直してみると 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるの茶 普通の公式が4×4× 円× 14=4円円の直径D=8cmです。よって円の面積Aは、 です(π=314で計算)。 円の直径から面積に変換する公式は、数学だけでなく物理や工学でも使います。必ず覚えておきましょう。直径、円の面積の詳細は下記が参考になります。 φと直径の関係は?




円の面積の公式 算数の公式




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト
円の方程式 中心:原点,半径:r の円の方程式 ; 円の面積の公式は「半径×半径×π(314)」のため、100φの円の面積は5×5×314=785cm2(平方センチメートル)と求めることができるのです。 続いて100φの円周の求め方も見ていきます。 円周の場合は直径×π(314)で計算できるため、10×314 =314cmがこれに三角形の面積は『底辺×高さ ÷2 ÷ 2 』です。 ここでは 「底辺:元の円の円周(直径×円周率)」 、 「高さ:元の円の半径」 にあたります。 また、直径を 2 2 で割ると半径になります。




円周の求め方 公式は直径を使うので 半径と間違えないように 中学や高校の数学の計算問題




Excel エクセルで円の面積から直径を計算したり 直径から面積を求める方法 Pi関数の使用方法
円 面積計算 公式 求め方 計算方法 直径 半径 自動 円周率 計算機 履歴機能付き 外接円の半径の公式 公式①正弦定理から求める 公式②3 辺と面積から求める 外接円の半径の求め方例題 外接円の性質 性質①外心(外接円の中心)と垂直二等分線 性質②外心と各頂点との距離 外接円の書き方 外接円の練習問題円周と直径の関係に着目して、円の面積を求める公式を変形します。 円周は直径に円周率を掛けたものに等しいので、 C = π d {\displaystyle C=\pi d} となります。



1




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく
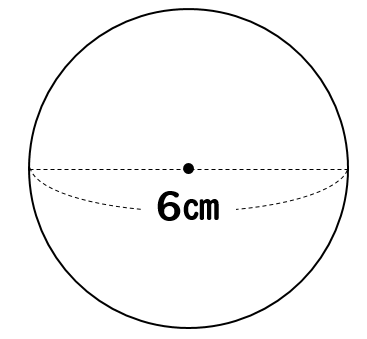
(1)円の面積を求める式、半径×半径×314にあてはめて、円の面積=3×3×314=26 (2)まず、半径の長さを先に求める。 半径は直径の半分だから、10÷2=5cm。 これを円の面積を求める式、半径×半径×314にあてはめて、円の面積=5×5×314=785中心:原点,半径:r の円の方程式 x 2 y 2 = r 2 r と θ を使って円周上の点Pを表すと, {x平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから)
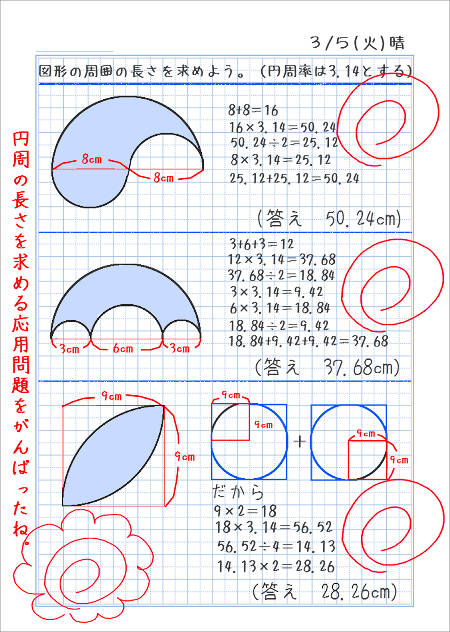



円周の長さの問題をもっと解いてみよう 家庭学習レシピ



中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su
半円 面積計算 公式 直径 半径 求め方 自動 円周率 area 面積: 半径から計算 半径: 面積: 円 円 半円 扇形 円周長から面積円 面積 直径 円 面積 直径 公式 直径の意味というより定義は「 円・楕円・双曲線で、中心を通り両端がその曲線上にある線分 」「 放物線では軸に平行な直線で放物線の内部にある半直線 」「 球では中心を通り両端が球面上にある線分 」となります。円の公式 円周・面積 円周率 = 36年「円の面積」 氏名 1 次の円の面積は何㎠ですか。 ⑴ 半径4cmの円 半径 × 半径 × 314 = 円の面積 式 答え ⑵ 半径8cmの円 式 答え ⑶ 直径14cmの円 直径 ÷ 2 = 半径 式 半径 × 半径 × 314 = 円の面積 答え ⑷ 直径18cmの円 式 答え



直径から円周の長さの求め方を解説 小学校 中学校でのそれぞれの計算方法は 数スタ




円 扇形 の面積 周や弧の長さの公式 数学fun
円の面積の求め方について円の面積を求める公式はπr²でしたよ 円の面積と公式 面積計算機 円 公式 直径 半径 自動 中1数学円柱の体積・表面積はどうやって求めるの? まな 円の面積の公式|「なぜ半径と円周率で求められるのか」を 工業のひし形の面積 対角線×対角線÷2=面積 a×b 2 1 a b 円の面積 半径×半径×314=面積 r ×r ×S=Sr 2 円の周りの長さ(円周) ①直径×314=円周 r ×2×S=2Sr 扇形の弧の長さと面積 360 x 円の直径の長さが4である円の面積を求めよ。 今回の問題は、公式に当てはめれば、半径が 4÷2 = 2 4 ÷ 2 = 2 なので 2 × 2× π = 4π 2 × 2 × π = 4 π これで終わりだよ




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
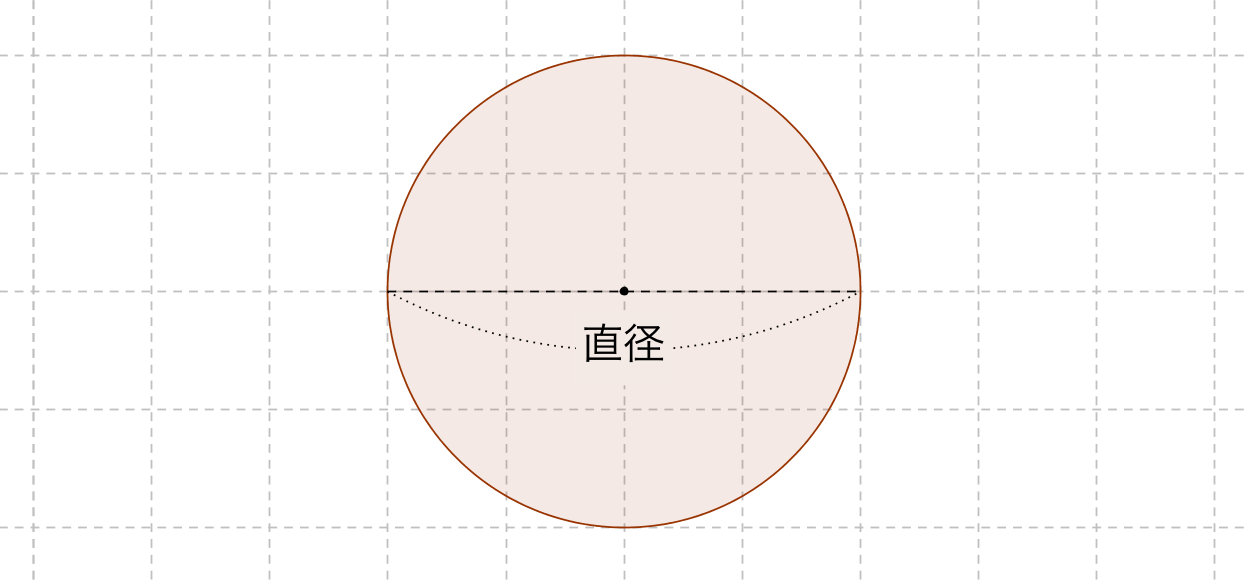



円周の公式 算数の公式
となった問題が。なんでも、円の直径の2乗が円の面積を表すというもの。なんのことやら? 円の面積というと 半径×半径×π ですよねぇ。 じゃあ、直径の2乗を計算してみましょう。 直径×直径 = (半径×2)×(半径×2) = 半径×半径×4 おや?円と球の公式 \(D\):直径 \(\rho\):密度 円の面積 \(\left ( \displaystyle \frac {\pi}{4} \right ) D^2\) 円周 perimeter \(\pi D\) 円形度 circularity (等面積円の円周)/(周長) 球の表面積(円の面積) = π r 2 という公式が作られる。 円の面積公式の、厳密な意味での証明は、三角関数の微分積分を待たなければならな い。しかし、この証明に出会える日本の高校生は、現行のカリキュラムでは非常に少ない。




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく



楕円の面積と公式 面積計算機
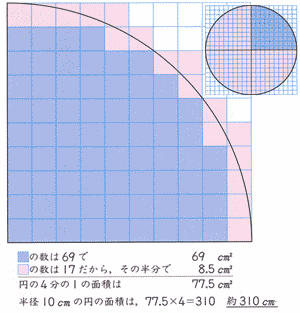
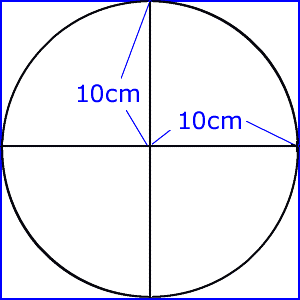
②円の面積の公式の理解 ③公式を使って、円の面積を求めること ④円や三角形をもとにして、曲線の図形の面積を求めること 教え方1 円の面積の大きさを順々に予想させていきます。 教え方1 半径10cmの円の内側と 円の外側に正方形をかいて、半径10cmの円内接円とは,三角形の3つの辺全てに接する円のこと。 内接円の半径は, S = r 2 ( a b c) S=\dfrac {r} {2} (abc) S = 2r (a b c) という公式を使って計算することができる。 三角形の内接円について詳しく解説します。 前半では,内接円の半径の計算公式の 円の面積の公式|「なぜ半径と円周率で求められるのか」を小学生に分かりやすく説明する方法 「なぜ公式で円の面積が計算できるの? 」 小学生のお子さんにうまく説明できずにいる人は多いと思います。
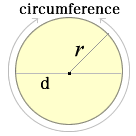



みんなの知識 ちょっと便利帳 円の面積から直径を計算する




インディアナ州円周率法案 Wikipedia
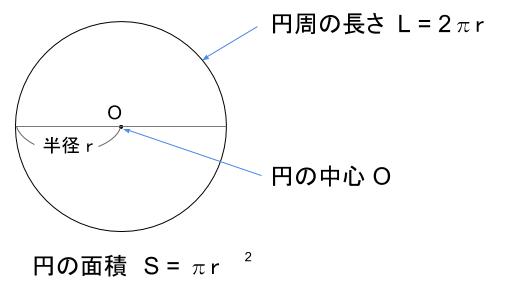
円の面積・直径・半径・円周の計算機。 公式を使った求め方も紹介。 円の面積と円周の長さを計算するツールです。 この計算機で出来ることは次の3つです。 直径・半径から、円の面積と円周の長さを求める。 円の面積から、直径・半径と円周の長さを求める。 円周の長さから、直径・半径と円の面積を求める。 計算には、javascriptライブラリ BigNumberjs を使用円の面積は 半径×半径×円周率=面積 で求めることができます。 半径をr、円周率をπ、面積をSとすると S=πr 2 となります。円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体
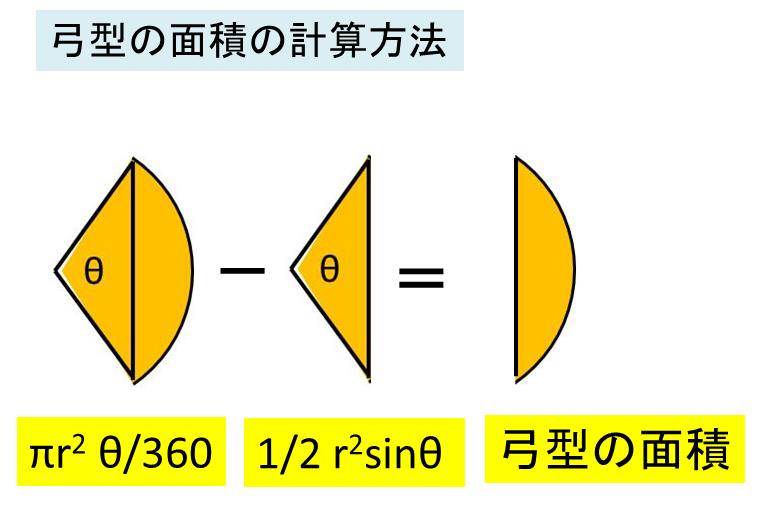



欠けた円 欠円 や弓形の面積の計算方法
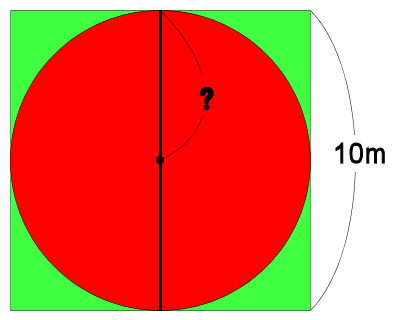



円の面積 直径




円の面積 円周の求め方 公式 小学生 中学生の勉強



円積率 雑学のソムリエ




円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ




円周から直径を求める Youtube




円の面積 算数用語集



13c5 Descubre Como Resolverlo En Qanda




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト
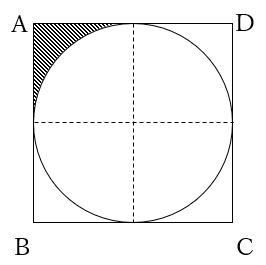



半径の分からない円の面積 中学受験プロ講師ブログ




中学数学が秒でわかる 円の面積を直径から求める 図付き なぜか分かる はかせちゃんの怪しい研究室




円の面積を求める 4つの方法 Wikihow




円周や円の面積を求めるときに使う円周率3 14ってなに みけねこ小学校



P 3 05を証明せよ 東大の伝説の入試問題をプログラムで解く 組み込みエンジニアの現場力養成ドリル 27 3 5 ページ Techfactory
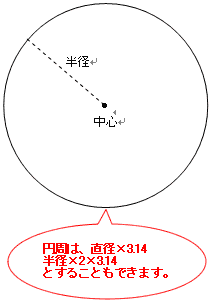



面積の考え方 算数の教え上手 学びの場 Com
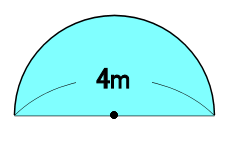



円の面積 半径



算数 三日月形 半円 の面積の応用問題の答 なるほどの素
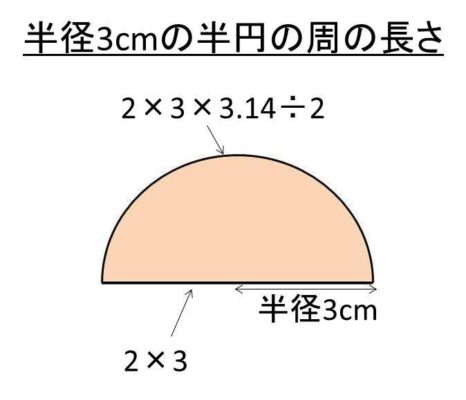



半円の周の長さの計算方法 モッカイ




円周の求め方 公式と計算例



実践記録算数5年
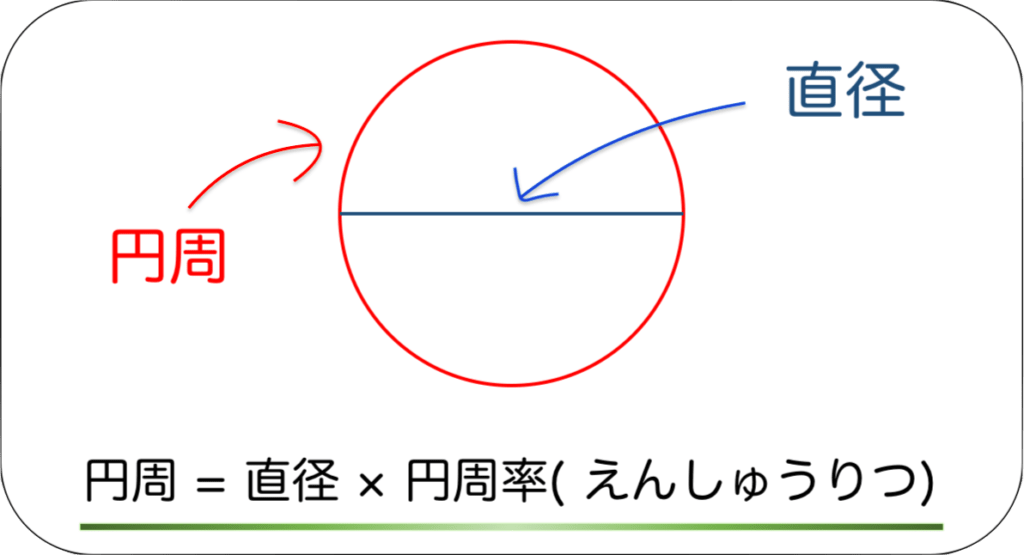



円 周 の 求め 方 ピクチャー ニュース




小6 算数 小6 旧 円の面積 Youtube
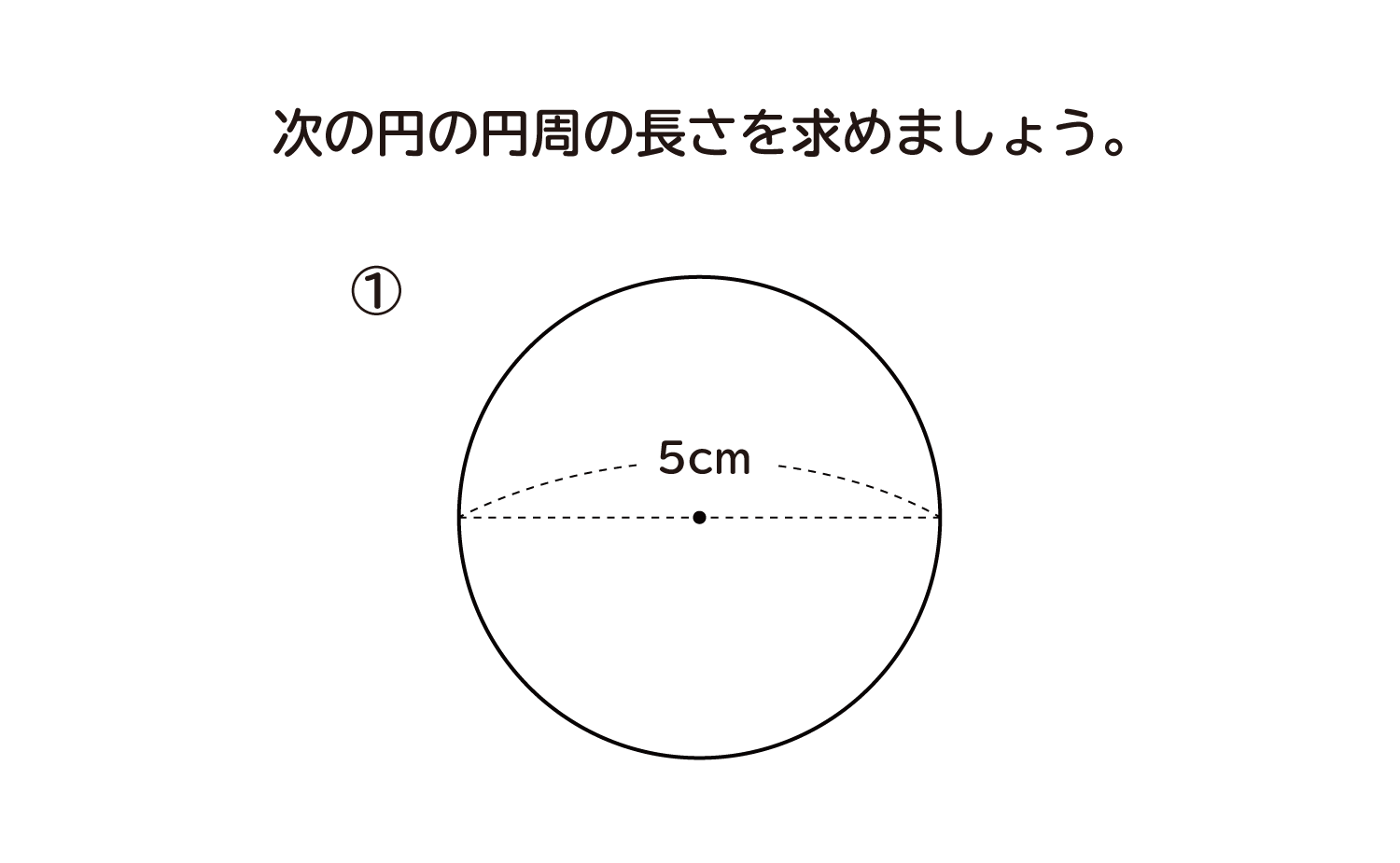



小学5年生 算数 無料問題集 円の直径と円周の長さ おかわりドリル




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく
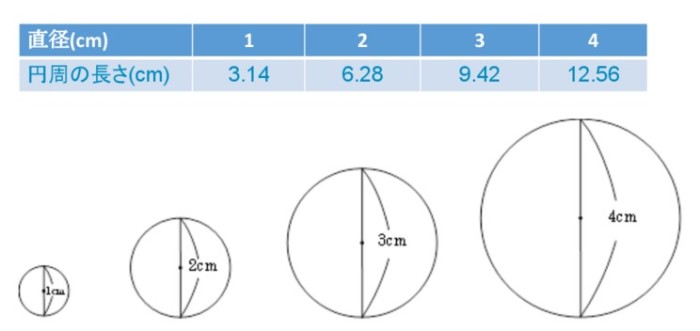



動画で学習 2 円周と直径 算数




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学



Search Q E5 86 86 E5 91 A8 E7 8e 87 Tbm Isch
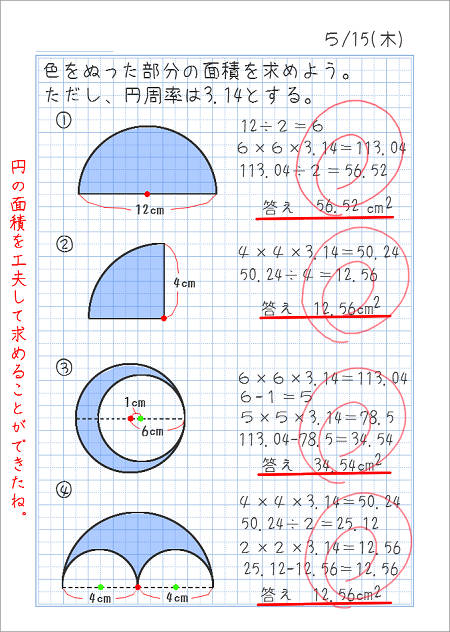



円の面積 その1 家庭学習レシピ



2




球の体積と表面積 公式と計算問題と証明 Irohabook



円の面積の求め方について円の面積を求める公式はpr でしたよね 1 4 P 直 Yahoo 知恵袋



3




実践記録算数5年



3




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




円の面積 円周の求め方 公式 小学生 中学生の勉強
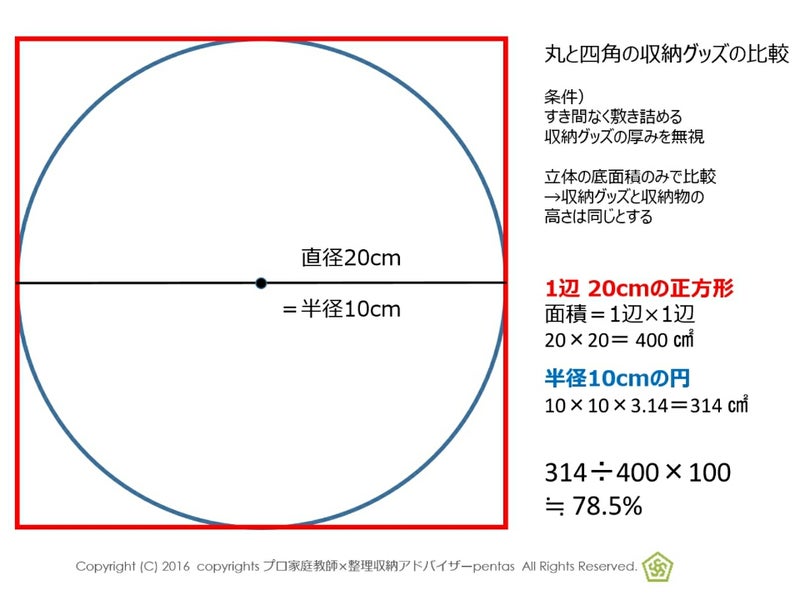



収納量の比較 数学の先生が 四角と丸の収納力を計算したら 中学受験から大学受験の塾プリント整理専門 プロ家庭教師 整理収納アドバイザー中島亜季 大阪京都奈良




円の直径を算出する方法 8 ステップ 画像あり Wikihow




円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun



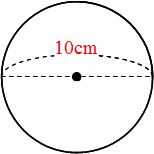
直径10cmの円の面積は 1分でわかる値 計算 直径と円の面積の関係



円の面積 円周の求め方 公式 小学生 中学生の勉強




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり



円を円で分割する比の法則 算数解法の極意



円の面積 直径から




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ
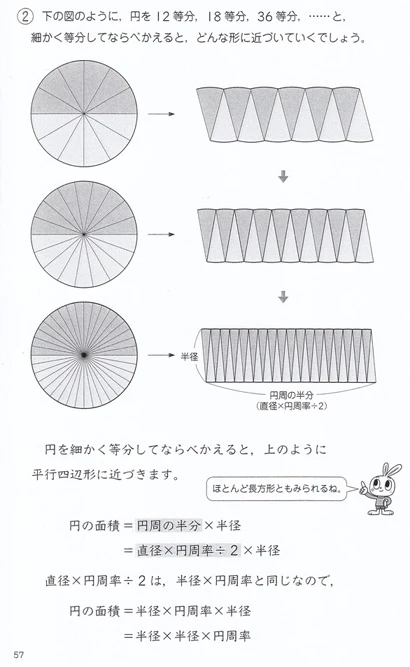



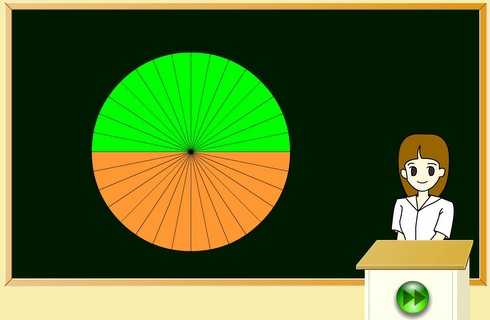
はるかさん 個人投資家 円を中心を起点にきめ細かい三角形に分割し 個々を互い違いに並び替えると 半径が縦の長さ 円周の半分が横の長さの長方形となる 円周の長さは直径 円周率 円周率の定義 円周の半分とは 半径掛ける円周率 直径の半分が



世界一やさしい 円の面積を求める問題の解き方 働きアリ



円の面積 直径



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ



円の面積の公式 算数の公式




ボード 豆知識 のピン




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




A B Barc D See How To Solve It At Qanda
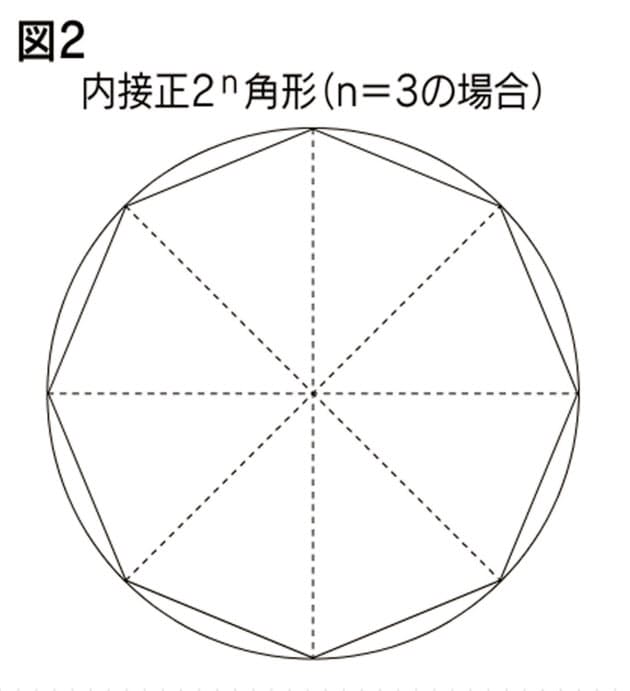



子供に説明できる 円の面積の公式 の証明 Nikkei Style
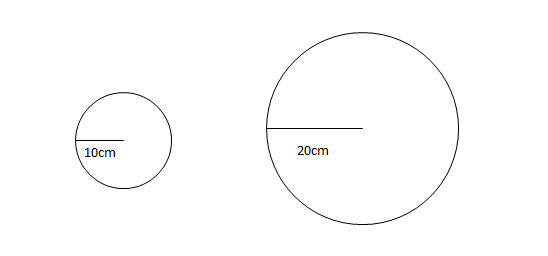



小学算数 円の半径と面積と円周の関係を理解しよう 偏差値40プログラマー



円の面積と公式 面積計算機




円の面積の求め方 公式と計算例




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



円周の公式 算数の公式




円の部分面積と部分円周を教えてください 添付にある円のcの面積と 数学 教えて Goo



円周率 P とは 求め方や100桁までの覚え方をご紹介 受験辞典
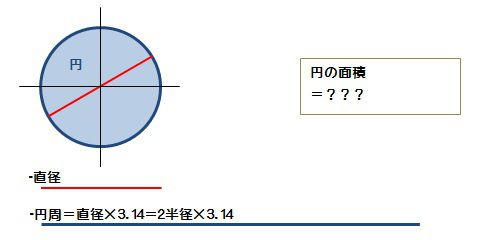



円の面積 算数の公式覚えてますか




6年算数 円の面積 1 アニメでわかる教え方




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun



6年算数 円の面積 1 アニメでわかる教え方




この問題がわからないのですが 誰か教えてくれますか 答えは 113 04 Clear



円の面積はなぜ 半径 半径 3 14 なの 一目で理由が分かるサイトが話題に ねとらぼ




円の面積 練習応用 Youtube




円周の求め方と円の面積について アタリマエ




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題



盲点の英単語 その8 円の面積の求め方を英語で言える 中学の英語をあなどってはいけない



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める



直径から面積に変換するには 1分でわかる計算 公式 直径の2乗との関係



世界一やさしい 円の面積を求める問題の解き方 働きアリ




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
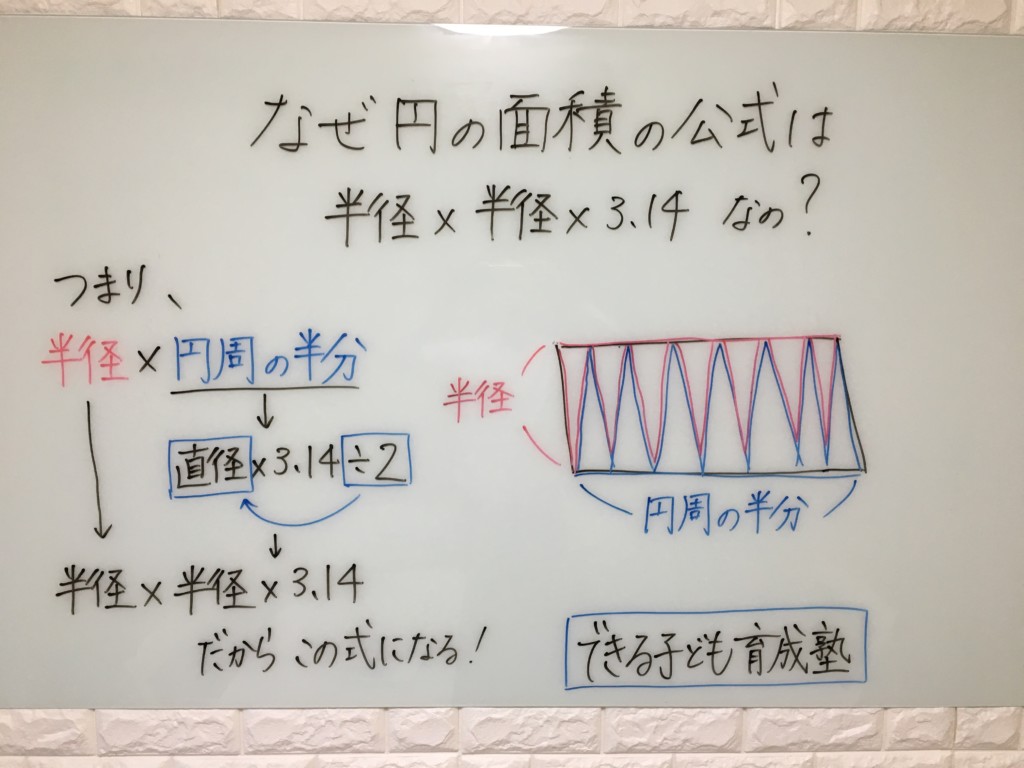



円の面積の求め方 公式 の理由を小学生に教える方法 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服




円の面積の求め方 公式と計算例



6年算数 円の面積 2 わかる教え方




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube



円の面積の求め方を教えてください 4分の1の大きさの円 です Yahoo 知恵袋



6年算数 円の面積 2 わかる教え方
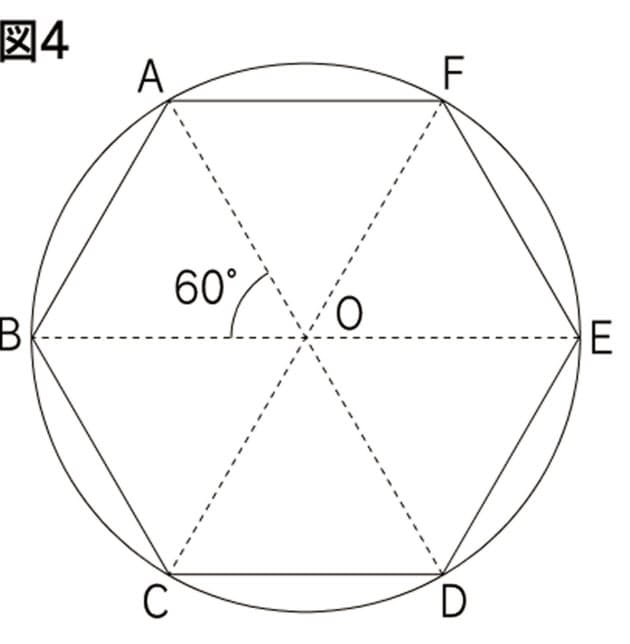



子供に説明できる 円の面積の公式 の証明 Nikkei Style
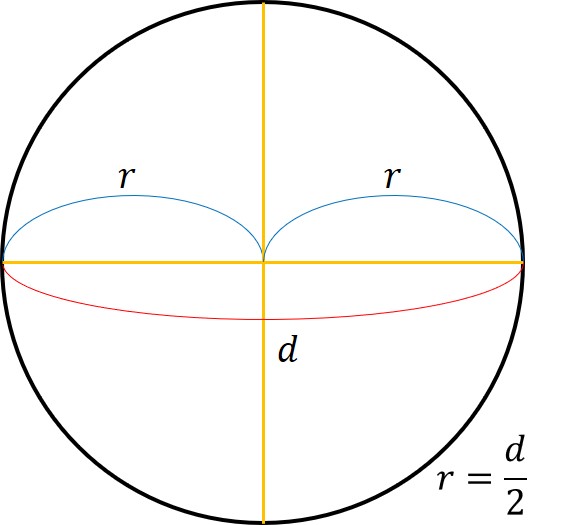



円の面積を求める公式 計算問題の解き方




直径がobの半円の面積と おうぎ形oab面積と 直径がoaの半円の面積の求め方を教え Clear
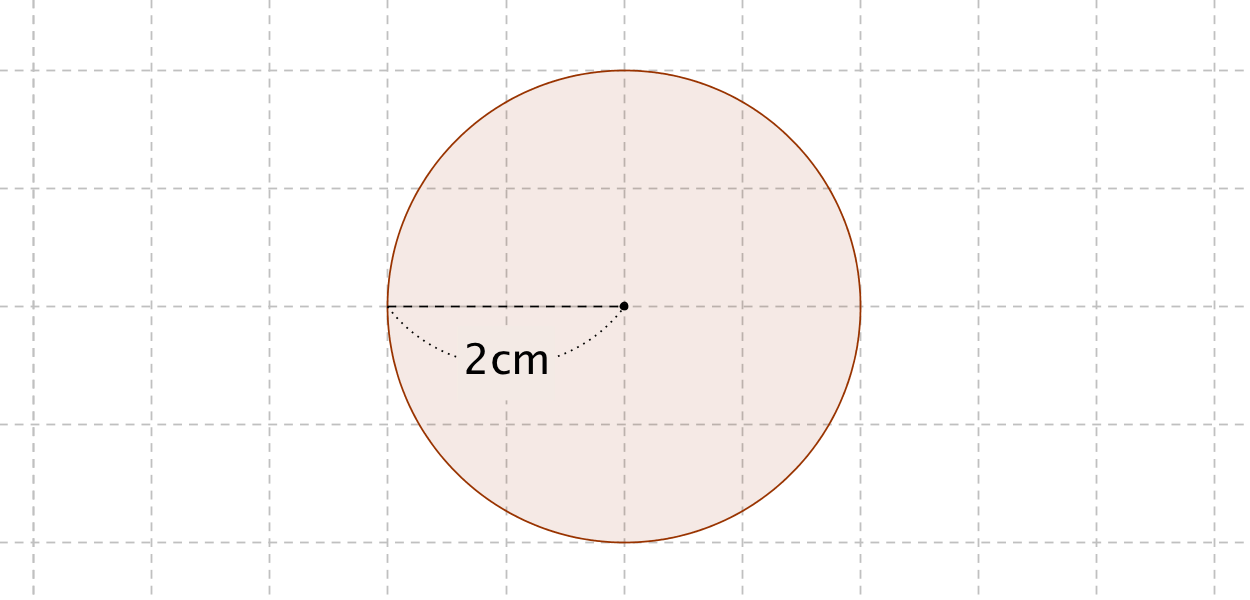



円の面積の公式 算数の公式




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




円の面積 算数用語集
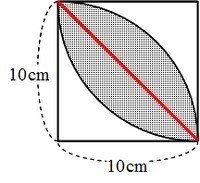



世界一やさしい 円の面積を求める問題の解き方 Shun Ei Note



0 件のコメント:
コメントを投稿