円錐の表面積の求め方!裏技の公式を覚えたらめちゃくちゃ簡単! 中学や高校の数学の計算問題 こんばんは、本日で長かった図形の公式 シリーズも終了です。 最後は円錐の表面積の公式です。 円錐円柱の表面積の解説 円柱の表面積を求めるには、まず上下の円の部分と側面の部分を分けて考えます。側面部分は筒状ですが、開いて四角形の状態にします。 円の面積は 半径×半径×円周率 なので円錐の表面積や体積の求め方!すぐ分かる方法を慶応生が解説!|高校生向け受験応援メディア「受験のミカタ」 ☝ ですが、これを活用しない限りは現状は変わらないです。 なお、円錐の表面積を出すときは少し考え方が複雑です。

現役塾講師直伝 円錐の表面積を求める 裏技 Kouの学び部屋
円錐 表面積 求め方 簡単
円錐 表面積 求め方 簡単- 円錐の側面積の求め方が分かりません。 図のような底面の半径が2cm、母線の長さが5cmの円錐の表面積を求めなさい。 という問題なのですが 表面積は求められるのですが、側面積が求め 表面積=9π+27π =36π (㎠) 以上です! めちゃくちゃ簡単じゃないですか? 以上のように、、「円錐の表面積」の問題は 公式1つでとても簡単になります。 それでは今すぐ上の円錐の表面積を "ボハンパイ"を用いて求めてみましょう!




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
円すいの表面積=半径×半径×円周率+母線×半径×円周率→6×6×314+10×6×314=96×314=(㎠) 今回は数値の設定上、 たまたま体積と表面積が同じ数値になりましたが、ただの偶然 です。学習事項:6章 空間図形 円錐の表面積 ・本時の目標 円錐の側面積の求め方について説明することができる。(思) ・本時の展開 教師の働きかけ( )・予想される生徒の反応( ) 留意点( )・評価(※) 1 問題の把握 次の図 予想しよう。円錐の側面積、底面積、表面積の求め方 😙 いずれにしても、これらの体積や表面積を計算できるようにならなければいけません。 そしてこの弧の長さを使えばおうぎ形のつまり側面の中心角、ひいては面積を出すことができます。
円柱Bの底面の半径が 3㎝のとき、円柱Bの表面積を求めなさい。 まずは円錐Bの高さを求めてみよう。高さをxと置いて、 円錐Aの体積=円錐Bの体積 という方程式を作ってxを求める。 そのあとに、円錐Bの表面積をいつも通り計算してやればいい 円すいの展開図、中心角の公式を知って5秒で解こう♪ 面積 面積 円すいの展開図の中心角を求めなさい。 円周率は314とします。 知りたがり 何に注目 すれば2:円錐の表面積の求め方 次は、円錐の表面積の求め方を解説します。 おそらく、この記事を見ているほとんどの人が ・解けなかった人 ・解けたけど時間がかかった人 だと思います。
側面積(扇形の面積)は,π×× nnn = 16 π 底面積と側面積(扇形の面積)を加えると,表面積は π (2) 底面は半径 3 の円だから,底面積は π×32= 9 π 展開図において扇形の中心角を x° とおくと,扇形の弧の長さが底面の円周の長さと等しくなるですが、次の方法で簡単に計算することができます。 円すいの側面積 = 母線 × 半径 × π 5 × 3 × π = 15 π c m 2 問題表面積を求めなさい。 表面積 = 側面積 底面積 底面積は 9 π c m 2 、側面積は 15 π c m 2 よって、表面積は 15 π 9 π = 24 π c m 2 この記事の目的:錐形を求める際に「3分の1」する理由を中学生にも分かるように説明する. はじめに 錐形は3分の1 指針 ①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積が変わると? 最後に




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題
足して円錐の表面積=a ( a b )πです。 こういうテクニックが数学ではたくさんあります。 興味のある方は是非無料体験してみてくださいね!前述の通り、円錐の表面積 S を求める公式は、次の通りです。 S = πr(r R) = π ×(底面の半径)× {(底面の半径) (母線の長さ)} S = π r (r R) = π × (底面の半径) × { (底面の半径) (母線No012 円錐の体積と表面積 円錐の体積 V m 3 円錐の底面の半径 r m 円錐の高さ h m 円錐の母線の長さ l m 円錐の底面の面積 S 1 m 2 扇形の中心角 θ deg 扇形の周の長さと円錐の底面の円周の長さは等しい 扇形の面積 S 2 m 2 円錐の表面積 S m 2 2




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく
円錐の表面積の公式 先に、公式が知りたい人のために公式をサクッと紹介 公式は S = πr(l r) S = π r ( l r) だよ! 記号の意味が分からない人は図も見てね 円錐の側面積の求め方ですね。 円錐の側面積の求め方 母線×底面の半径×314 確かにこの公式を覚えておけば側面積を即答できるため、圧倒的に有利なのですが、それは覚えていられる間の話。 もし 忘れたり混乱したりすると、求められなくなって これで展開図の長方形のよこの長さがわかり、求めたい円柱の側面積がわかりますね。 底面の円周(長方形のよこの長さ)は 2×3×π=6π cm 円柱の側面積は 8×6π=48π cm 2 底面積は 3×3×π=9π cm 2




円錐の表面積の求め方 公式と計算例
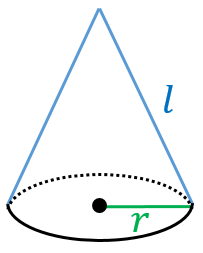



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S底面積とは?1分でわかる意味、求め方、円錐、三角錐、四角柱 円柱の側面積は?1分でわかる求め方、公式、底面積と表面積、体積との関係 まとめ 今回は円柱の表面積について説明しました。意味が理解頂けたと思います。底面である円の面積をそれぞれ求めて 合計してやれば、表面積の完成です! それぞれ計算してやると 側面積は $$\pi \times8^2\times \frac{135}{360}$$ $$=64\pi \times \frac{3}{8}$$ $$=24\pi$$ 底面積は $$\pi \times 3^2=9\pi$$




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
円錐の体積と公式の問題、高さの求め方 下図の円錐の体積を、公式を用いて求めましょう。 上記の値を公式に当てはめれば良いので簡単ですね。 また下図の円錐の体積=15m 3 、半径=2mのとき 1分でわかる意味、体積の公式と例題の求め方、表面積 円周 = 2× 6 ×π = 12π 円 周 = 2 × 6 × π = 12 π だから、 こんな感じになるね! 扇形と円で比例式を立てて、 4π 12π = x 360 4 π 12 π = x 360 ∴ 12π× x = 4π× 360 12 π × x = 4 π × 360 ∴ x = 4π 12π × 360 x = 4 π 12 π × 360 ∴ x = 1 x = 1 だから、1°だね! はかせちゃん 面積: 円錐、角錐・・・底面積×高さ×3分の1 円柱、角柱・・・底面積×高さ 表面積:すべての面の面積を足せばどれも求めることができます。ただ、円錐、円柱の場合はわかりにくいので、一度展開図にしてから計算しなければなりません。




空間図形14 円すい台の体積 Youtube




円錐の体積ってなんであの公式なの Webty Staff Blog
円錐の表面積 次に円錐の表面積についてです。 以下の図のような円錐の表面積を求めてみましょう。 先程と同様に展開図を考えます。 すると、おうぎ形が側面、円が底面となります。 底面積と側面積を合わせたものが表面積であるのでそれぞれ求めて




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



1




円錐の表面積を簡単に求める方法 Easy Way To Find The Surface Area Of A Cone Youtube




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




表面積の求め方 計算公式一覧




中学数学 裏技伝授 1分で解ける円錐の表面積 中心角の求め方 ニコニコ動画




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




球の表面積と体積の公式 数学fun




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




円錐の表面積の求め方 公式と計算例




この円錐の体積と表面積の求め方を教えてください Clear




現役塾講師直伝 円錐の表面積を求める 裏技 Kouの学び部屋




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




表面積の求め方 計算公式一覧




中学1年生 数学 無料問題集 円すいの表面積 おかわりドリル




角錐 円錐の体積と表面積の公式 数学fun



Studydoctor円錐の表面積の求め方 中学1年数学 Studydoctor




円錐の表面積 Youtube




球の表面積と体積の公式 数学fun
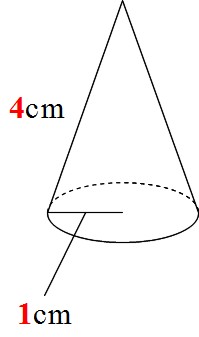



Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ




円錐の表面積 簡単な求め方とその理由を解説するぞ 中学数学 理科の学習まとめサイト




円錐の体積ってなんであの公式なの Webty Staff Blog




中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室




公式を図解 すい体の体積 円すいの表面積の求め方




表面積の求め方 計算公式一覧




円錐の表面積の求め方 You Look Too Cool




公式を図解 すい体の体積 円すいの表面積の求め方
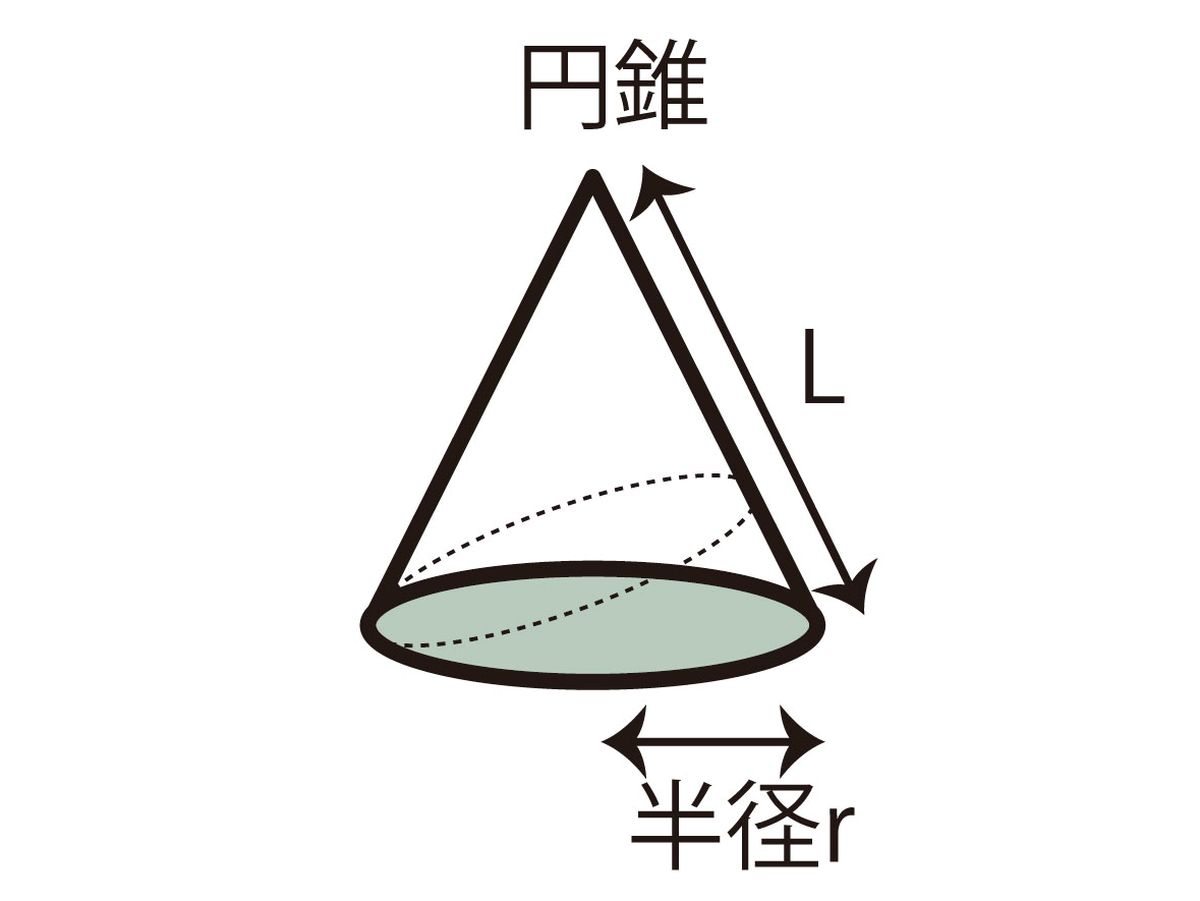



円錐の側面積の公式を理解させる方法 オンライン授業専門塾ファイ




裏ワザ公式 円すいの側面積を一瞬で求める方法 Youtube




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




毎日問題を解こう 27 苦手な数学を簡単に



三角錐とは 体積 表面積の公式や求め方 受験辞典
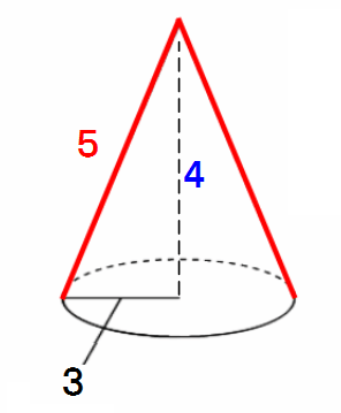



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
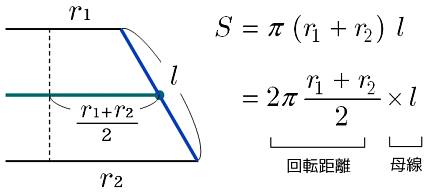



初等幾何 円錐台の側面積を求める 大人が学び直す数学




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




円錐の表面積 あんず学習塾のメモ 図表置き場




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



底面の半径が5cmで母線の長さが9cmの円錐の表面積の求め方を教えてくださ Yahoo 知恵袋




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
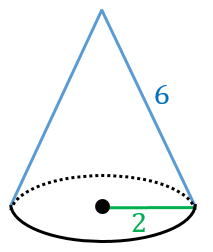



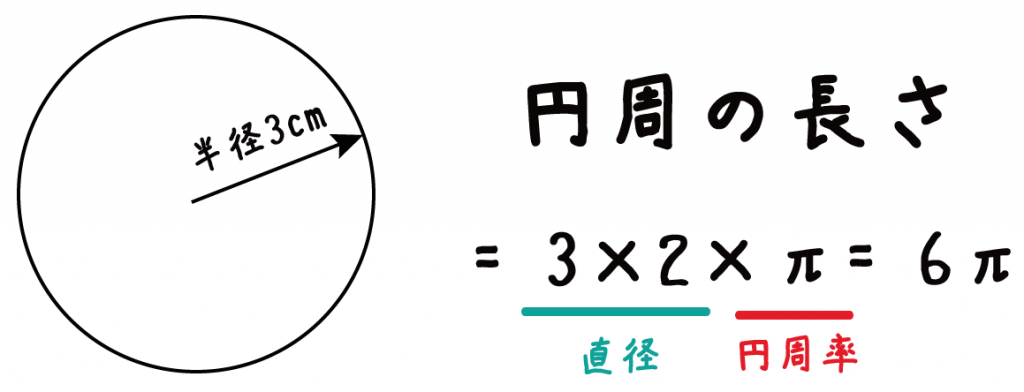
円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




公式を図解 すい体の体積 円すいの表面積の求め方




表面積の求め方 計算公式一覧
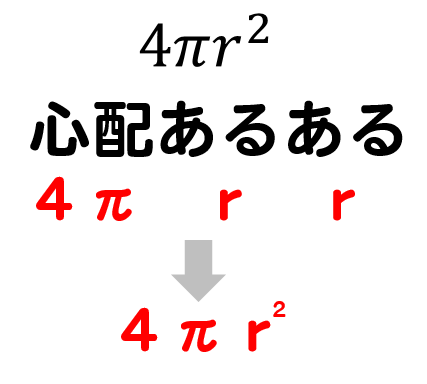



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者
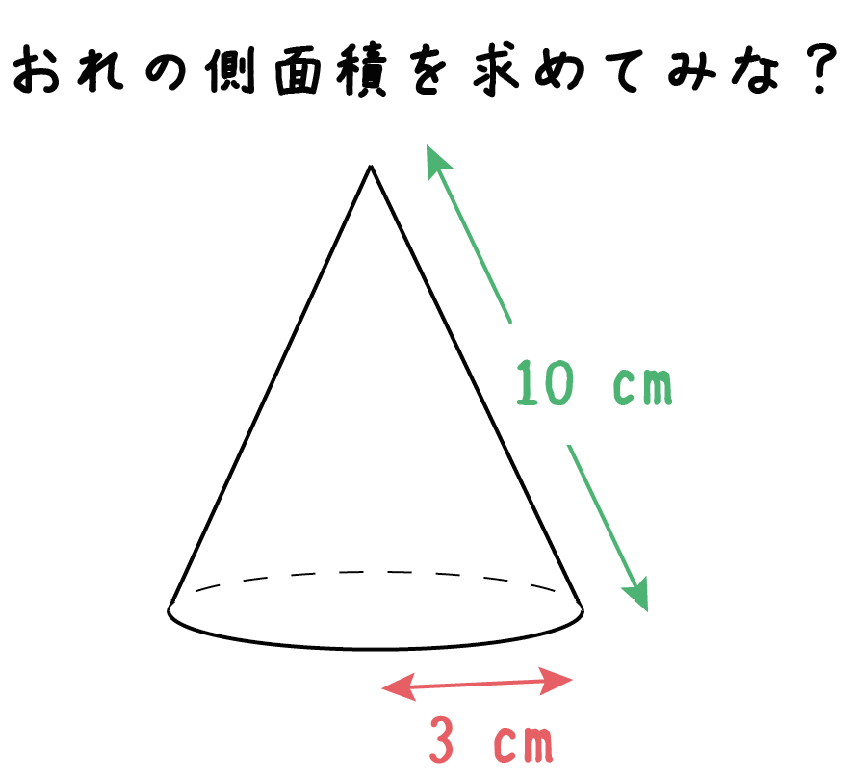



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学 円すいの表面積 中学数学の無料オンライン学習サイトchu Su
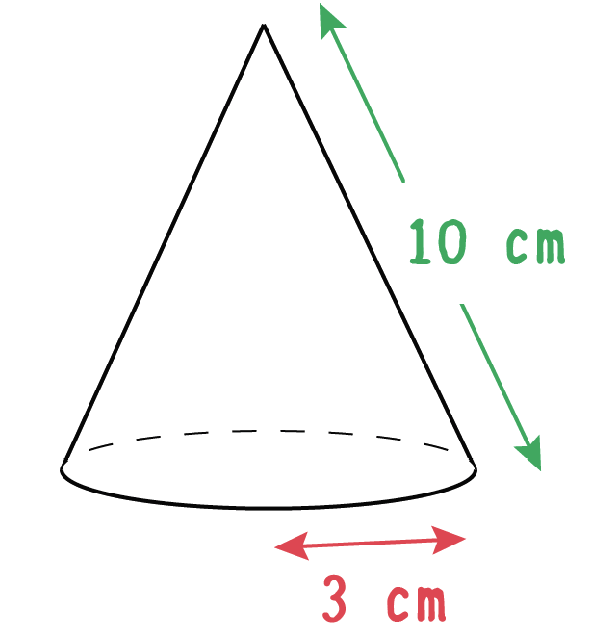



計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積の求め方 公式と計算例




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室




円すいの展開図 表面積の求め方 公式があるの知っていますか




球表面積公式證明妙不可言的數學證明 Qavhp




球の体積と表面積 公式と計算問題と証明 Irohabook




3分でわかる 円錐の体積 表面積の求め方 合格サプリ
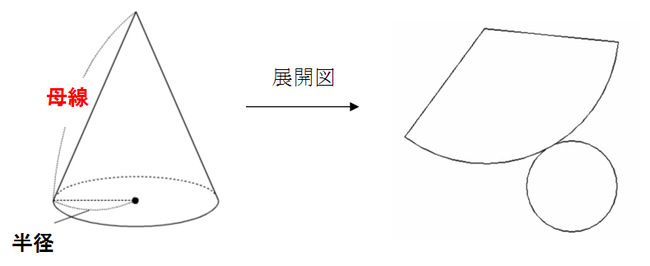



数学公式の最強裏技一覧 中学生や高校生の方はぜひ見て 三重の個人契約家庭教師



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方



円錐の側面積の求め方が分かりません 図のような底面の半径が2cm 母線 Yahoo 知恵袋




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com
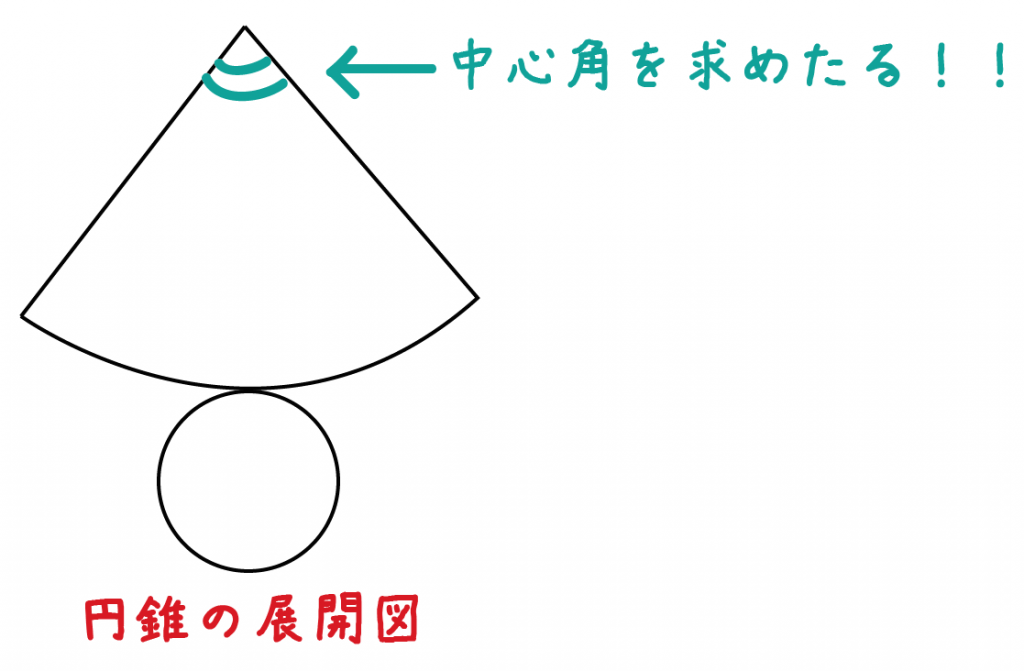



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



円錐とは 体積 表面積の公式や求め方 受験辞典




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット
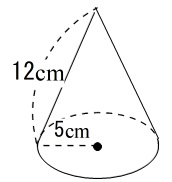



円錐 すい の表面積や四角錐 五角錐の体積の求め方




この問題の円錐の底面積の半径の求め方を教えてください Clear




円錐の表面積 側面積 体積の求め方教えてください Clear




円錐の表面積 Youtube




Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ



円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明



円錐の側面積の求め方 インターネット家庭教師のアスミラ



1
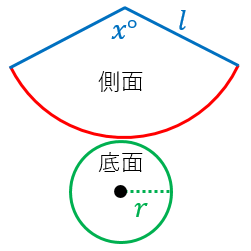



円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
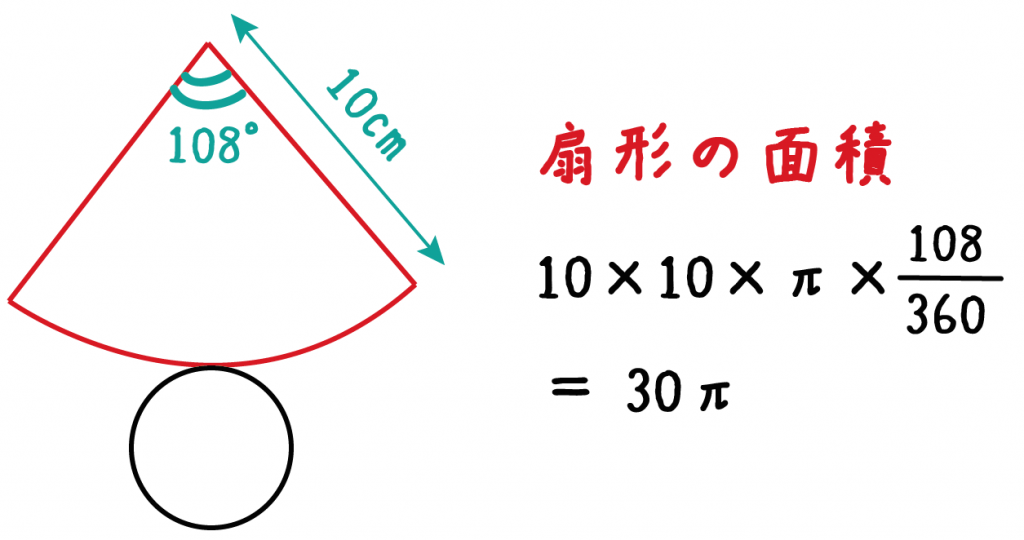



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1



1




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット




円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




円錐の表面積 側面積 体積の求め方教えてください Clear




この円錐の表面積の求め方を教えてください Clear



0 件のコメント:
コメントを投稿