Free Parabola Vertex calculator Calculate parabola vertex given equation stepbystep This website uses cookies to ensure you get the best experienceI have an equation right here it's a second degree equation it's a quadratic and I know it's graph is going to be a parabola this was a review that means it looks something like this or it looks something like that because the coefficient on the x squared term here is positive and it's going to be an upwardopening parabola and I am curious about the vertex of this parabola and if I haveA parabola is a plane curve where any point is at the same distance from the focus and the directrix The general equation of a parabola is {eq}{y^2} = 4ax{/eq} or {eq}{x^2} =
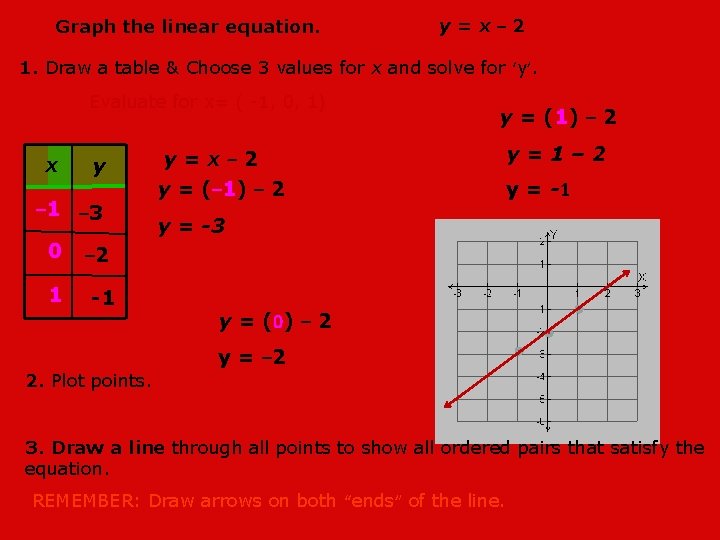
Graph The Linear Equation Yx 2 1 Draw
Y=(x-h)^2+k parabola
Y=(x-h)^2+k parabola-Graphing Parabolas Part 4 Graphing Recap Graphing by Completing the Square Intro Graphing by Completing the Square How Graphing by Completing the Square Freaky Things That Can Happen Making the Connection Between Graphing and Solving Coolmath privacy policy Find the slope of the tangent to the parabola y = x ^ 2 at the point (2,4) univerkov education The slope of the tangent to the graph of the function f (x) at the point with coordinates (x0;



Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download
Show that the coordinates of the centroid G of the area between the parabola y = \frac{x^2}{a} and the straight line y = x are \overline{x} = \frac{a}{2} , \overline{y} = \frac{2 a}{5}Graph the parabola y= (x5)^2 4 2 Rotating the parabola y = x2 by θ clockwise gives v = u2, where (u v) = (cosθ − sinθ sinθ cosθ)(x y) ie xsinθ ycosθ = (xcosθ − ysinθ)2 Putting θ = π 4 gives 1 √2(x y) = ( 1 √2(x − y))2√2(x y) = (x − y)2 which when expanded is x2
Answers Click here to see ALL problems on Rationalfunctions Question 444 graph the parabola y= (x5)^2 4 Answer by venugopalramana (3286) ( Show Source ) You can put this solution on YOUR website!The Parabola Given a quadratic function f ( x) = a x 2 b x c, it is described by its curve y = a x 2 b x c This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation y = x 2 − 4 x 5Y0) is equal to the value of the derivative of this function at x = x0
Finding the focus of a parabola given its equation If you have the equation of a parabola in vertex form y = a (x − h) 2 k, then the vertex is at (h, k) and the focus is (h, k 1 4 a) Notice that here we are working with a parabola with a vertical axis of symmetry, so the xcoordinate of the focus is the same as the xcoordinate of the vertexConsider the parabola of equation y = x2 and a point P = (h, h2) arbitrary on it, where h 0 (see figure) Q (0yo) Pch h) (0) Determine the equation of the line L1 that is tangent to the parabola by P 2) Determine the equation of the line L2 that is perpendicular to L1 and passes through P 3) If Q = (0, ya) is the point of intersection of L20 votes 2 answers The equation of a tangent to the hyperbola 4x^2 5y^2 = parallel to the line x y = 2 is



Solution Graph The Parabola Y X 4 2 2




How To Graph Y X 2 1 Youtube
The parabolas y 2 = 4x and x 2 = 4y divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes If S 1, S 2 and S 3 are respectively the areas of these parts numbered from top to bottom, then S 1 S 2 S 3 is equal to (a) 1 y = √ x (the top half of the parabola);Parabola problems with answers and detailed solutions, at the bottom of the page, are presented Questions and Problems Find the x and y intercepts, the vertex and the axis of symmetry of the parabola with equation y = x 2 2 x 3?;




Example 1 Graph A Function Of The Form Y Ax 2 Graph Y 2x 2 Compare The Graph With The Graph Of Y X 2 Solution Step 1 Make A Table Of Values For Ppt Download




Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
One formula works when the parabola's equation is in vertex form and the other works when the parabola's equation is in standard form Standard Form If your equation is in the standard form y = a x 2 b x c , then the formula for the axis of symmetry is x = − b 2 a Vertex FormWe're going to explore the equation of a parabola y=a x 2 b xc for different values of a, b, and c First, let's look at the graph of a basic parabola y=x 2 , where a =1, b =0, and c =0 Notice the graph opens up, the vertex is at x=0, and the yintercept is at y=0Solution (2) ⅓ The given two curves are parabola y = x 2 and y 2 = x The point of intersection of these two parabolas is 0 (0, 0) and A (1, 1) as shown in the figure y 2 = x or y = √x – f (x) y – x 2 = g (x) where f (x) ≥ g (x) in 0, 1 Required area = = ∫ 0 1 f ( x) − g ( x) d x = ∫ x − x 2 d x = 2 3 x 1 / − x 3 3 0 1 = 2 3 − 1 3 = 1 3



Graph Y X 2 Youtube
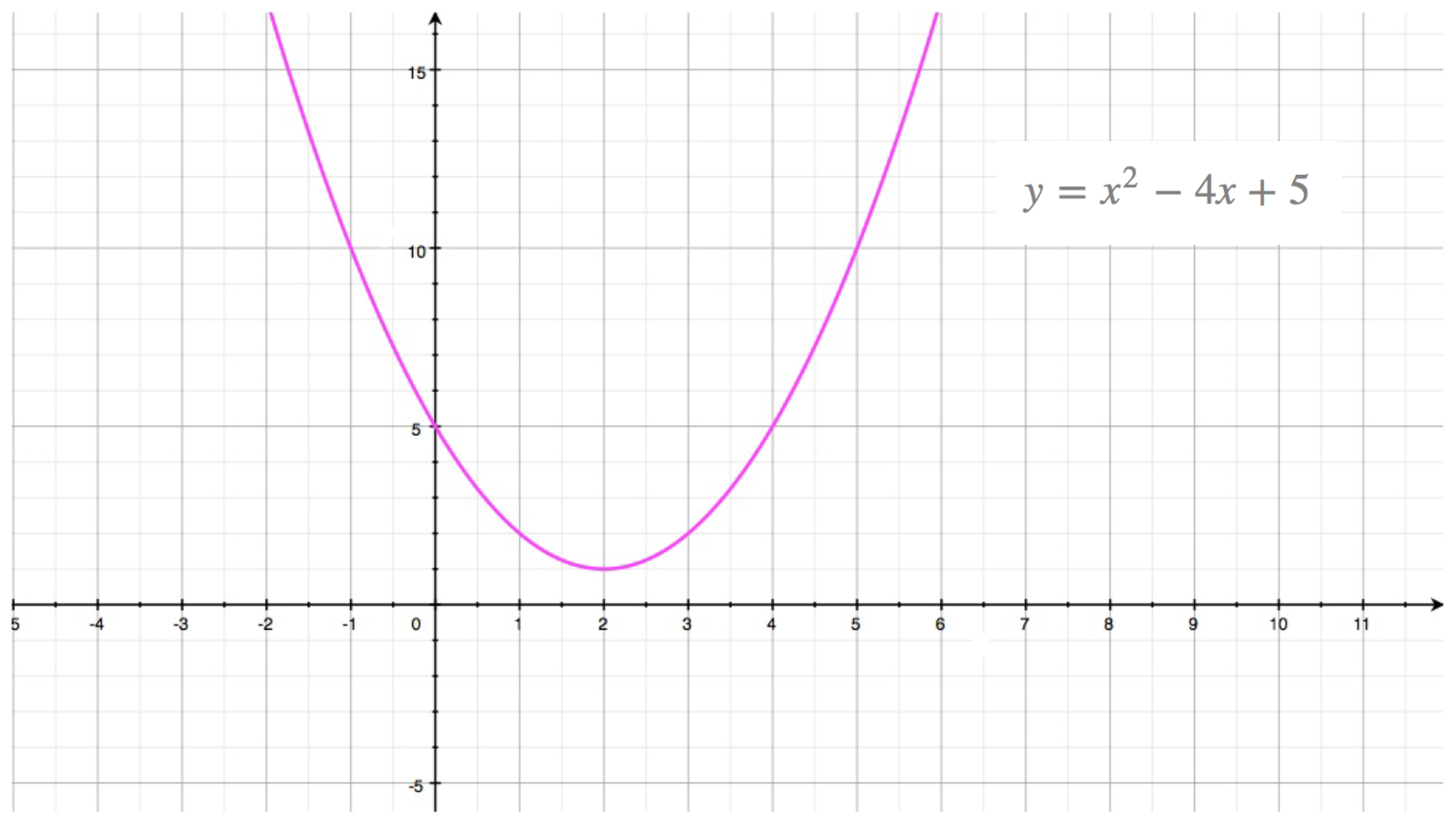



Quadratic Function Parabola
Parabola Hyperbola A parabola is defined as a set of points in a plane which are equidistant from a straight line or directrix and focus The hyperbola can be defined as the difference of distances between a set of points, which are present in a plane to two fixed points is a positive constantTo find the roots and axis of symmetry of y = x 2 − 3 x without graphing, use factoring (or the distributive law), as follows The roots are where y = 0, so we have x 2 − 3 x = 0 which factors into x ( x − 3) = 0 So, x = 0 OR x − 3 = 0 → x = 3 Roots The roots of y = x 2 − 3 x are 0 and 3 Axis of symmetry The axis of symmetryFor m = 1, y = x 2, so the equation of the tangent perpendicular to the given tangent is y = − x − 2 The required point is the point of intersection to there tangents ie, ( − 2 , 0 ) Alternately perpendicular tangents to a parabola intersect on the directrix, x 2 = 0



Solution Graph Y X 2 1 Label The Vertex And The Axis Of Symmetry And Tell Whether The Parabola Opens Upward Or Downward
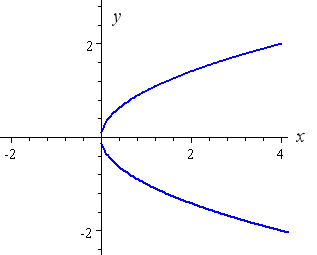



How To Draw Y 2 X 2
Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axis at DGood question If you are using an equation for lgebra/quadratics/transformingquadraticfunctions/v/shiftingandscalingparabolas Consider a parabola y = x^2 Answer the following questions and fill in your responses in the corresponding boxes on the answer sheets (1) the line that goes through the point (0, 3/2) and is orthogonal to a tangent line to the part of parabola y =



Practice Exam 1




Solution For The Parabola Y X 2 36 Graph Of A Parabola Opening Down At The Vertex 0 36 Crossing The X Axis At 6 0 And 6 0
translate Since the density of a plate at each point placed on the area bounded by the x=y line in the plane with the y = x^2 parabola, proportional to 30 times the distance of that point from the xaxis, if the center of gravity of the plate (x,y) is x=?Y=05x^2, y=2/3x^2 y=ax^2 is wider than y=x^2 if a is any real number greater than 0 but less than 1 if a is greater than 1 then it will be narrowed If a is negative then it will open downward Let P be the point of intersection of the common tangents to the parabola y^2 = 12x and the hyperbola 8x^2 – y^2 = 8 asked in Mathematics by Jagan (211k points) jee mains 19;
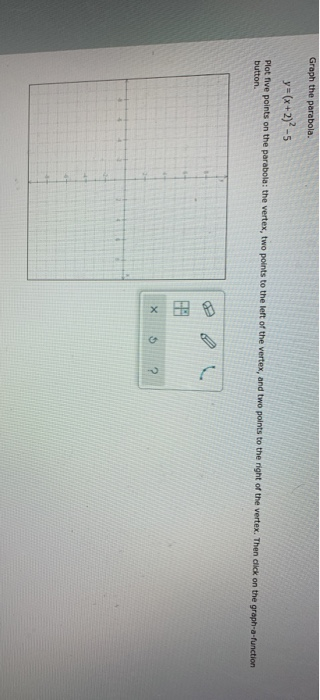



Graph The Parabola Y X 2 2 5 Plot Five Points On Chegg Com



Draw The Graph Of Y X 2 X And Hence Solve X 2 1 0 Sarthaks Econnect Largest Online Education Community
Graphing Basic Parabola Y X 2 Youtube For more information and source, see on this link https//myoutubecom/watch?v=qgFZ6SBs6UcGraph y=x^2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for The directrix of a parabola is the horizontal line found by subtracting from the ycoordinate of the vertex if the parabola Finding the yintercept of a parabola can be tricky Although the yintercept is hidden, it does exist Use the equation of the function to find the y intercept y = 12 x 2 48 x 49 The yintercept has two parts the xvalue and the yvalue Note that the xvalue is always zero So, plug in zero for x and solve for y y = 12 (0) 2 48 (0) 49 (Replace x with 0)




Quadratic Function
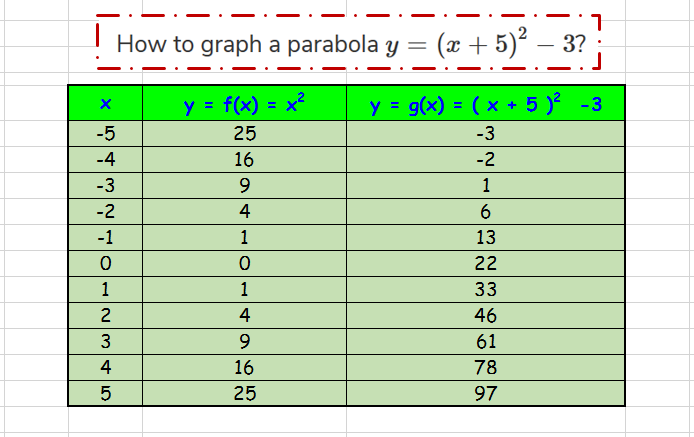



How To Graph A Parabola Y X 5 2 3 Socratic
Take the proportionality constant k vector space translate The surface S is the part of theX = − y 2 x = y 2 x = − y 2 x = y 2 Use the vertex form, x = a ( y − k) 2 h x = a ( y k) 2 h, to determine the values of a a, h h, and k k a = − 1 a = 1 h = 0 h = 0 k = 0 k = 0 Since the value of a a is negative, the parabola opens left Opens Left Find the vertex ( h, k) ( h, k)Step 1 Solve for the vertex of the parabola The vertex of a parabola of the form {eq}y= x^2 bx c {/eq} is always given by {eq}\left (\dfrac {b} {2a},f (\dfrac {b} {2a})\right) {/eq} Step



1



Graph Of F X 2 Y 2 Geogebra
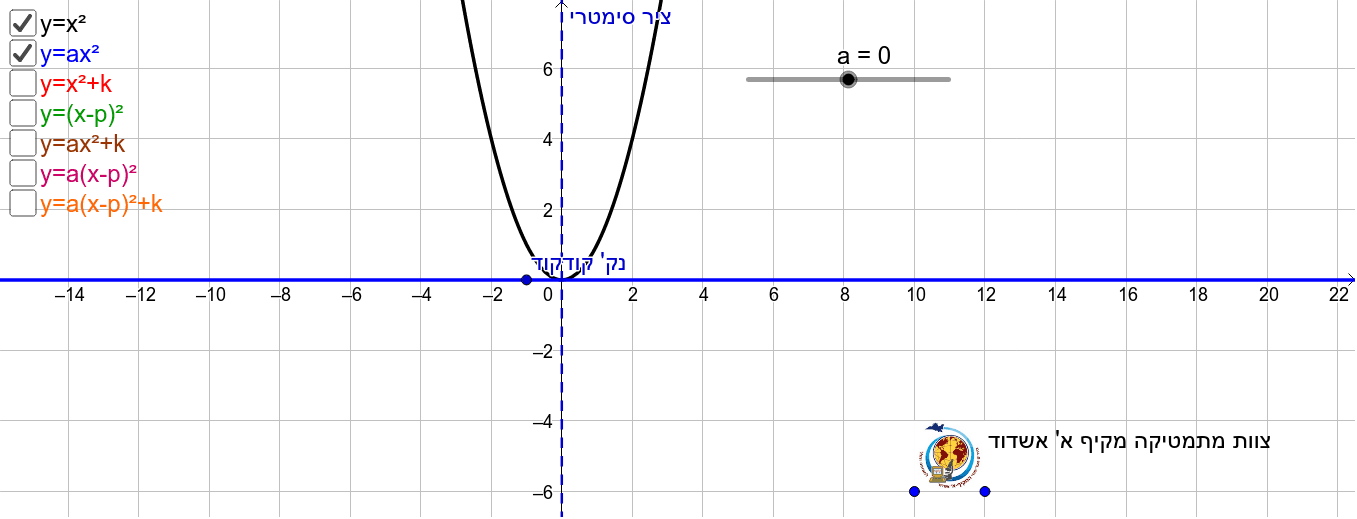
Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open downExploring Parabolas y = ax^2 bx c Exploring Parabolas by Kristina Dunbar, UGA Explorations of the graph y = a x 2 b x c In this exercise, we will be exploring parabolic graphs of the form y = a x 2 b x c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the thirdY = a x 2 b x c But the equation for a parabola can also be written in "vertex form" y = a ( x − h) 2 k In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y



Y X 2 2
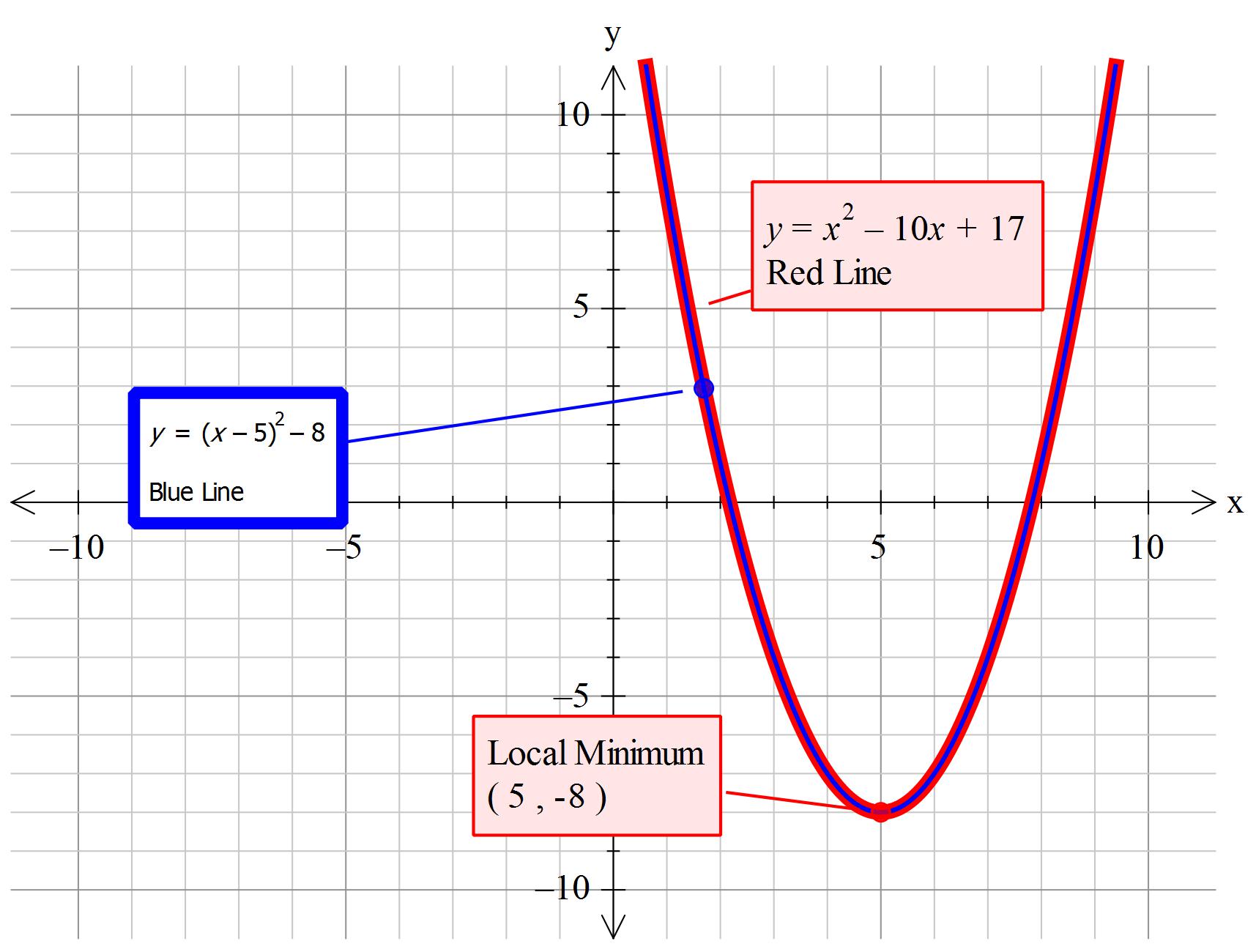



How Do You Write The Vertex Form Equation Of The Parabola Y X 2 10x 17 Socratic
The vertex form of a parabola's equation is generally expressed as y = a (xh) 2 k If a is positive then the parabola opens upwards like a regular "U" If a is negative, then the graph opens downwards like an upside down "U" If a < 1, the graph of the parabola widens This just means that the "U" shape of parabola stretches out sidewaysGraph of y = x 2 The shape of this graph is a parabola Note that the parabola does not have a constant slope In fact, as x increases by 1, starting with x = 0, y increases by 1, 3, 5, 7, As x decreases by 1, starting with x = 0, y again increases by 1, 3, 5, 7, Graphing y = (x h) 2 k In the graph of y = x 2, the point (0, 0) is called the vertex The vertex is the minimum point in a parabola #color(blue)("Some observations")# The #x^2# is positive so the general graph shape is #uu# Consider the generalised form of #y=ax^2bxc# The #bx# part of the equation shifts the graph left or right You do not have any #bx# type of value in your equation So the graph is central about the yaxis The #c# part of the equation is of value 1 so it lifts the vertex up



Math Spoken Here Classes Quadratic Equations 3



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4
Volume of a Parabola Rotated Around a Line The question is as follows Find the volume of the solid generated by revolving the region bounded by the parabola y = x 2 and the line y = 1 about the line y = − 1 My attempt Using the washer method, I set the outer radius to 1 x 2 and the inner radius to be 1 This gives me the integral VFoci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=x^{2} en Related Symbolab blog posts My Notebook, the Symbolab wayAnd y = −√ x (the bottom half of the parabola) Here is the curve y 2 = x It passes through (0, 0) and also (4,2) and (4,−2) Notice that we get 2 values of y for each value of x larger than 0 This is not a function, it is called a relation



Solution I Do Not Know How To Graph The Parabola Y X 2



Content Transformations Of The Parabola
This is a simple case First, use FOIL (x ?) (x?) That must be the case The factors of 5 that add up to 6 are 5 and 1, so these are your factors They must be positive, because every coefficient is positive So your final result is (x5)(x1)The two parabolas y 2 = 4ax and x 2 = 4ay intersect y 2 =4ax, x The two parabolas y 2 = 4ax and x 2 = 4ay intersect A at two points on the line y = x B only at the origin C at three points one of which lies on y x = 0 D only at (4a, 4a) Please scroll down toOn the parabola y = x^2, the point at a least distance from the straight line y = 2x 4 is



How To Draw Y 2 X 2




File Parabola Y X 6x 7 Svg Wikimedia Commons
What are the points of intersection of the line with equation 2x 3y = 7 and the parabola with equation y = 2 x 2 2 x 5? The vertex form of the equation of a parabola is y=(x3)^236 what is the standard form of the equation rosieweber04 rosieweber04 Mathematics High School answered The vertex form of the equation of a parabola is y=(x3)^236 what is the standard form of the equation 2 See answersPositive quadratic y = x^2 Negative quadratic y = x^2 Parabola (concave up) The vertex (p,q) is the minimum point when a parabola is concave up In this case y =q is the minimum value and so the range is R = { y e R y > q } Parabola (concave down) The vertex (p,q) is the maximum point for a parabola when it is concave down In this case y = q is the maximum value and so the range is R = { y e R y < q } Symmetrical Points The axis of symmetry cuts a parabola




Topological Variation For The Offsets Of The Parabola Y X 2 Download Scientific Diagram



Y X 2 12x 35 Math Homework Answers
The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetry



Y X 2 2



Solution How To Graph A Parabola Using Y X2 2x 8



Parabolas




Graph The Linear Equation Yx 2 1 Draw



Quadratics Graphing Parabolas Sparknotes



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2



Q Tbn And9gctwl8ksal48ks9fvcggchq7ifw Mt5nzxx1 0ivsjobxia io Usqp Cau



Quadratics



How To Write The Vertex Of The Parabola Y X 2 8x 10 Quora
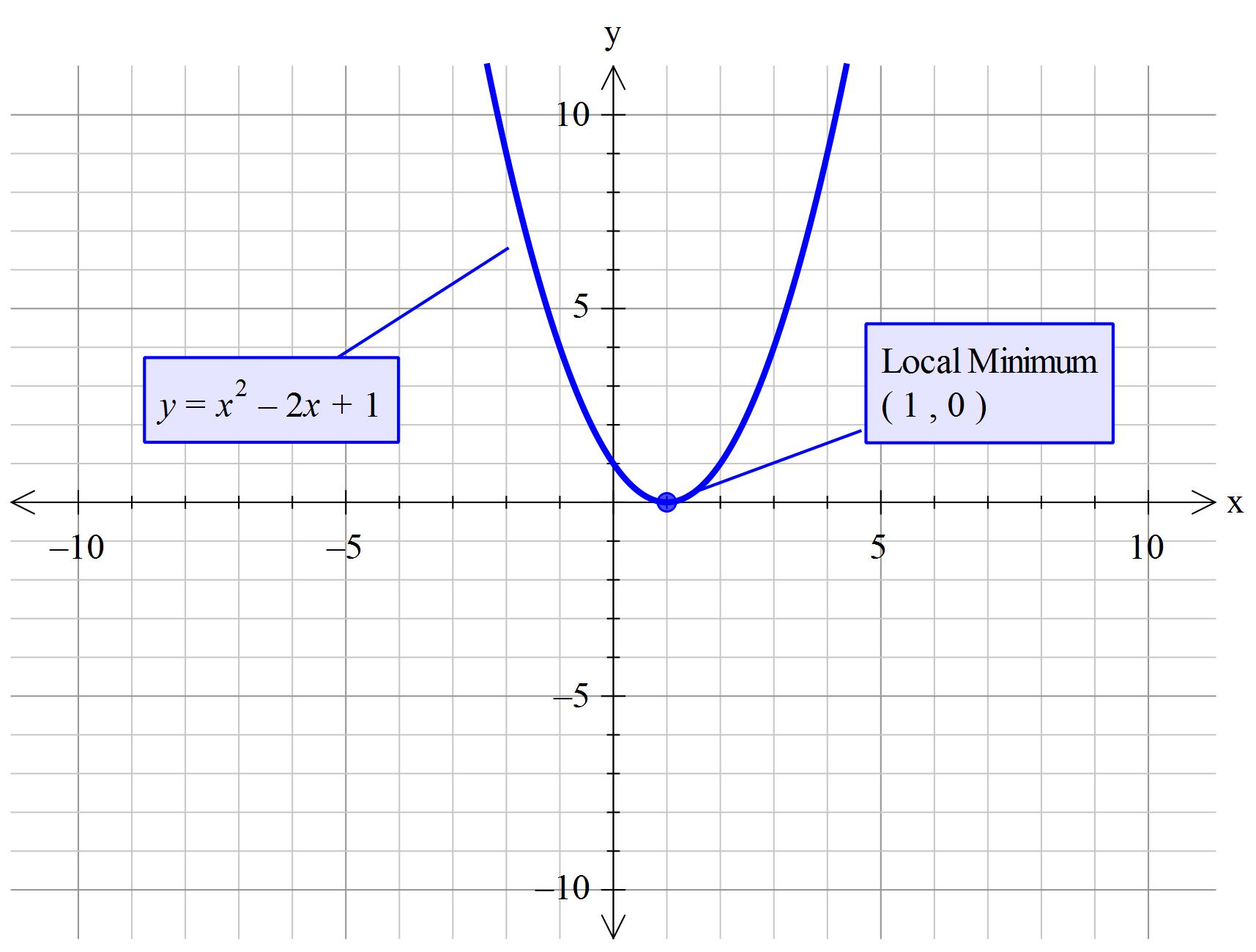



What Is The Vertex Of Y X 2 2x 1 Socratic



Content Transformations Of The Parabola
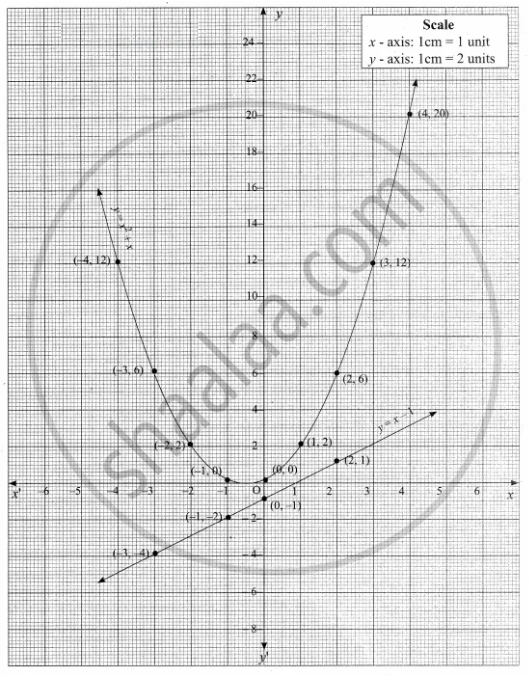



Draw The Graph Of Y X2 X And Hence Solve X2 1 0 Mathematics Shaalaa Com



Exploration Of Parabolas



How Do You Graph Y X 2 5x 3 Socratic




How Do You Graph Y X 2 1 Socratic




Consider The Parabola Y X 2 The Shaded Area Is Brainly In



Find The Area Of The Region Enclosed By The Parabola X2 Y And The Line Y X 2 Studyrankersonline
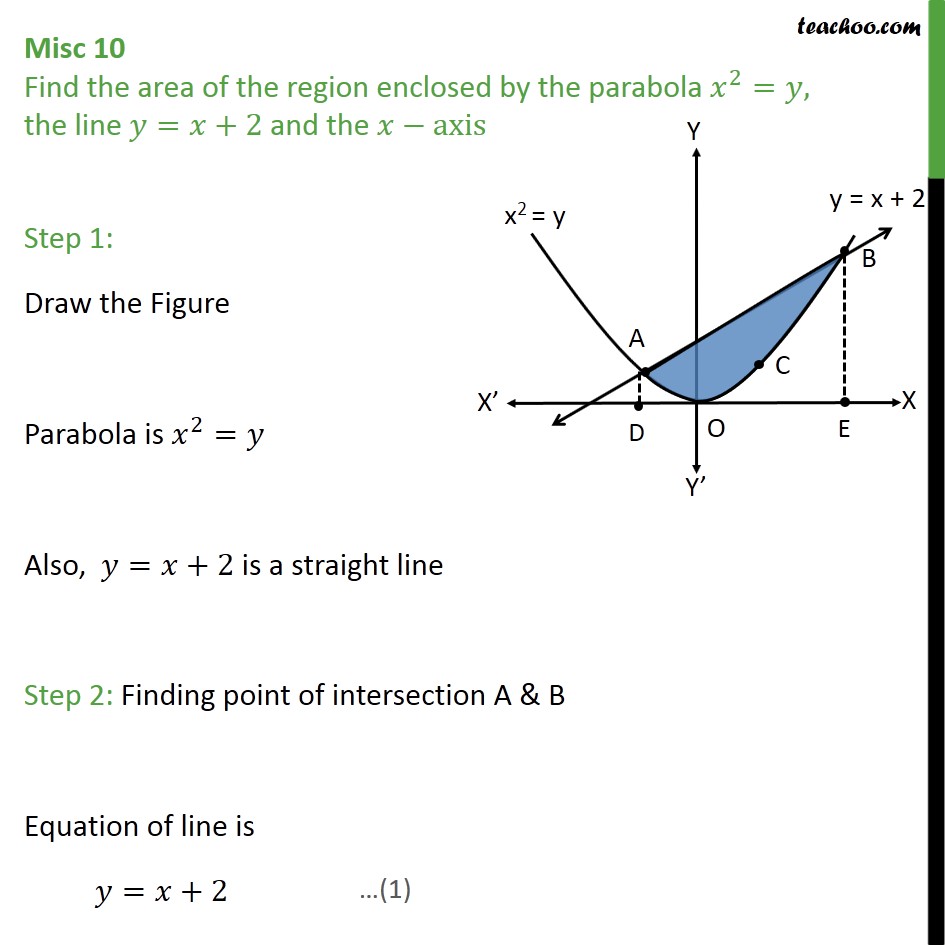



Misc 10 Find Area Enclosed By Parabola X2 Y T X 2



How Do You Graph Y X 2 9 Socratic




The Graph Of The Quadratic Function Y X2 Is Shown Below If This Parabola Is Reflected About The Brainly Com




Three Tangent Lines To The Parabola Y X 2 Corresponding To Three 1d Download Scientific Diagram
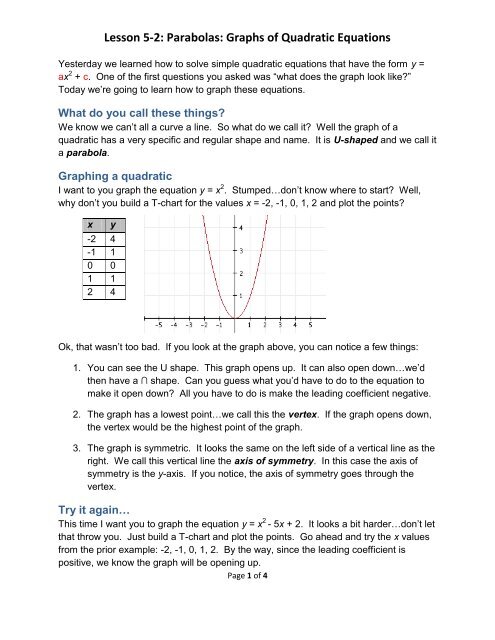



Lesson 5 2 Parabolas Graphs Of Quadratic Equations



Quadratics Graphing Parabolas Sparknotes



Transformations To The Graph Of Y X 2 Geogebra



Exploration Of Parabolas
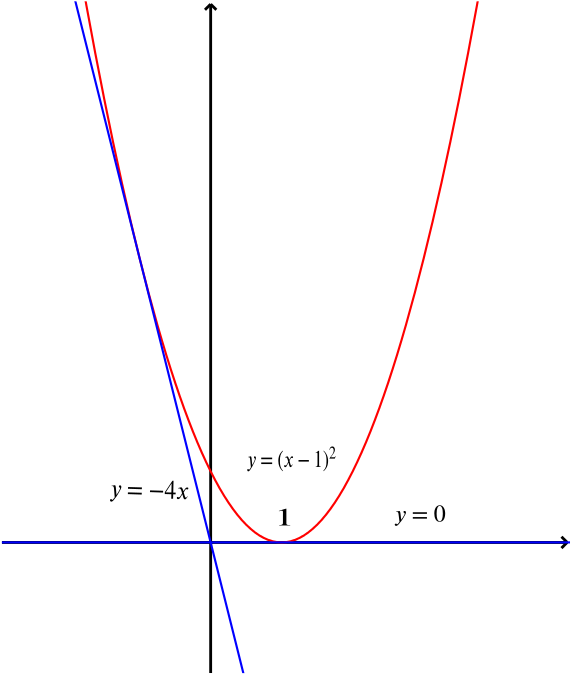



Solution When Does Y Kx Intersect The Parabola Y X 1 2 Quadratics Underground Mathematics
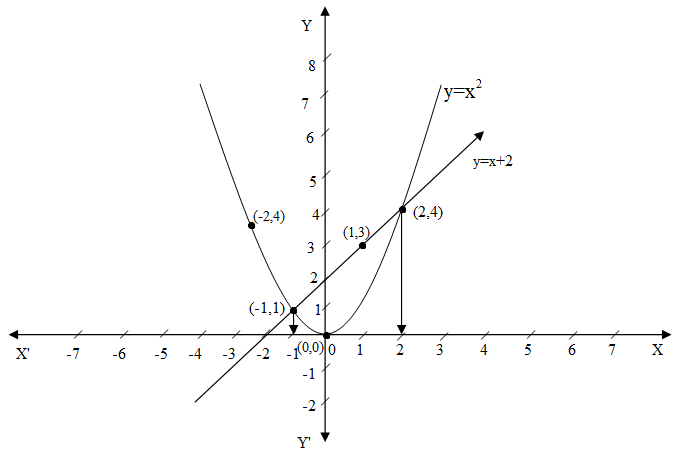



Draw The Graph Of Y X2 And Y X 2 And Hence Solve Class 10 Maths Cbse




How To Draw Y 2 X 2
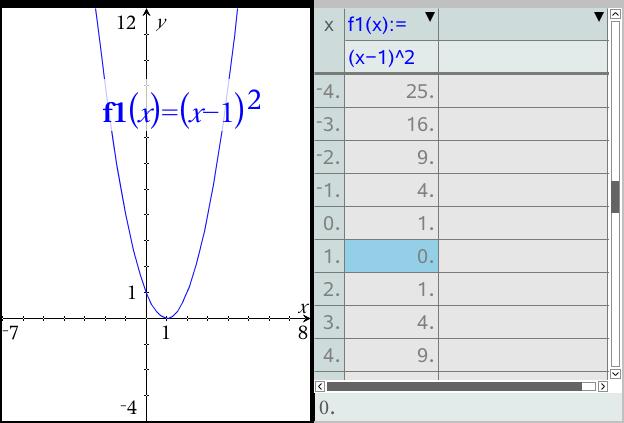



How Do I Graph The Quadratic Equation Y X 1 2 By Plotting Points Socratic



Where Do Y X 2 4x 1 And Y 3 X Intersect Mathskey Com
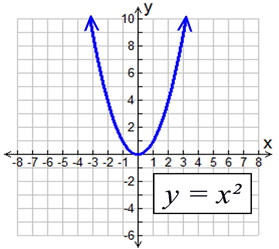



Parabola Parent Function Mathbitsnotebook A1 Ccss Math




Plot A Graph For The Equation Y X 2 4x 1
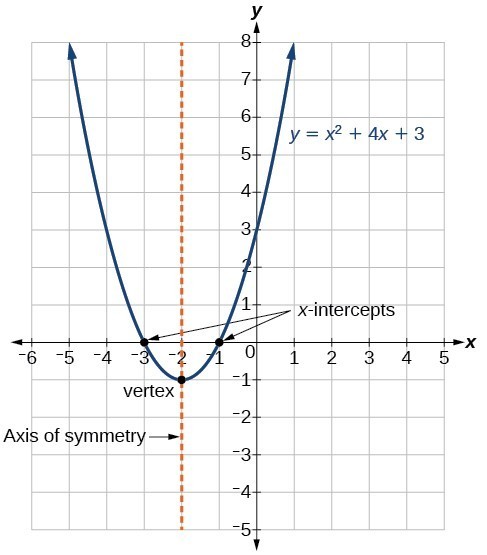



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra



How Do You Sketch The Graph Of Y X 2 2x And Describe The Transformation Socratic



The Line Y 2x 9 Is Tangent To The Parabola Y X 2 Ax B At The Point 4 1 What Are The Values Of A And B Quora



Parabola Y X 2 Geogebra




B Examine The Graph Of Th Lihat Cara Penyelesaian Di Qanda



Graphs Of Functions Y X2 Y 2x2 And Y 2x2 In Purple Red And Blue Respectively




Example 15 Find Area X Y 0 Y X2 1 0 Y X 1
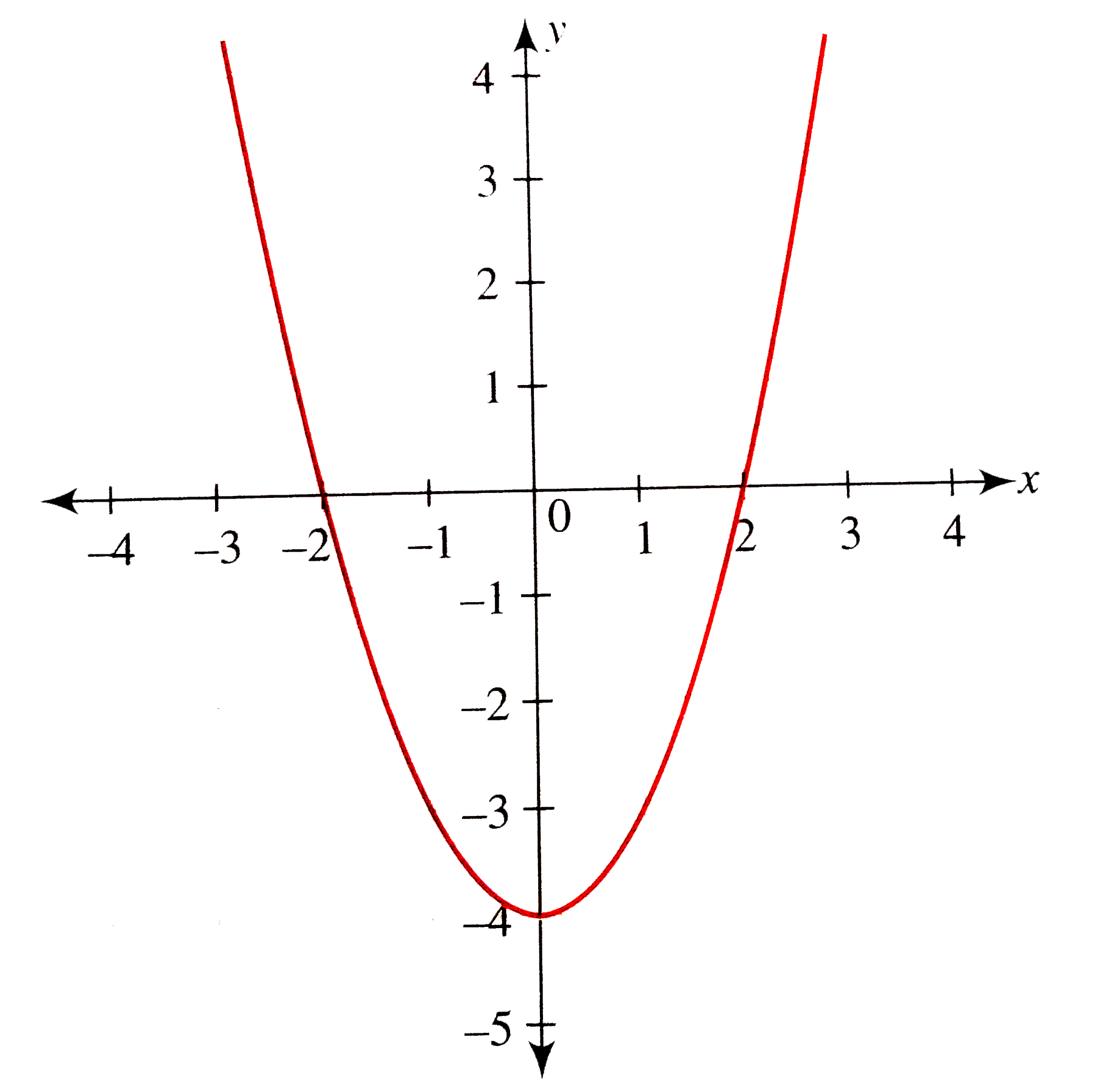



From The Graph Of Y X 2 4 Draw The Graph Of Y 1 X 2 4




The Area Bounded By The Parabola Y 4x 2 Y X 2 9 And The Li




Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




Graph Of Parabola Y X 2 Novocom Top




Graphing Parabolas




Y X 2



Quadratics Graphing Parabolas Sparknotes




Find The Area Of The Region Bounded By The Parabola Y X 2 And Y X
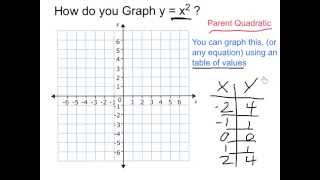



Graph Y X 2 Youtube



Content Transformations Of The Parabola




Graph Y X 2 3 Youtube



Quadratics




How To Graph A Parabola Of The Form Y X 2 Bx C Algebra Study Com
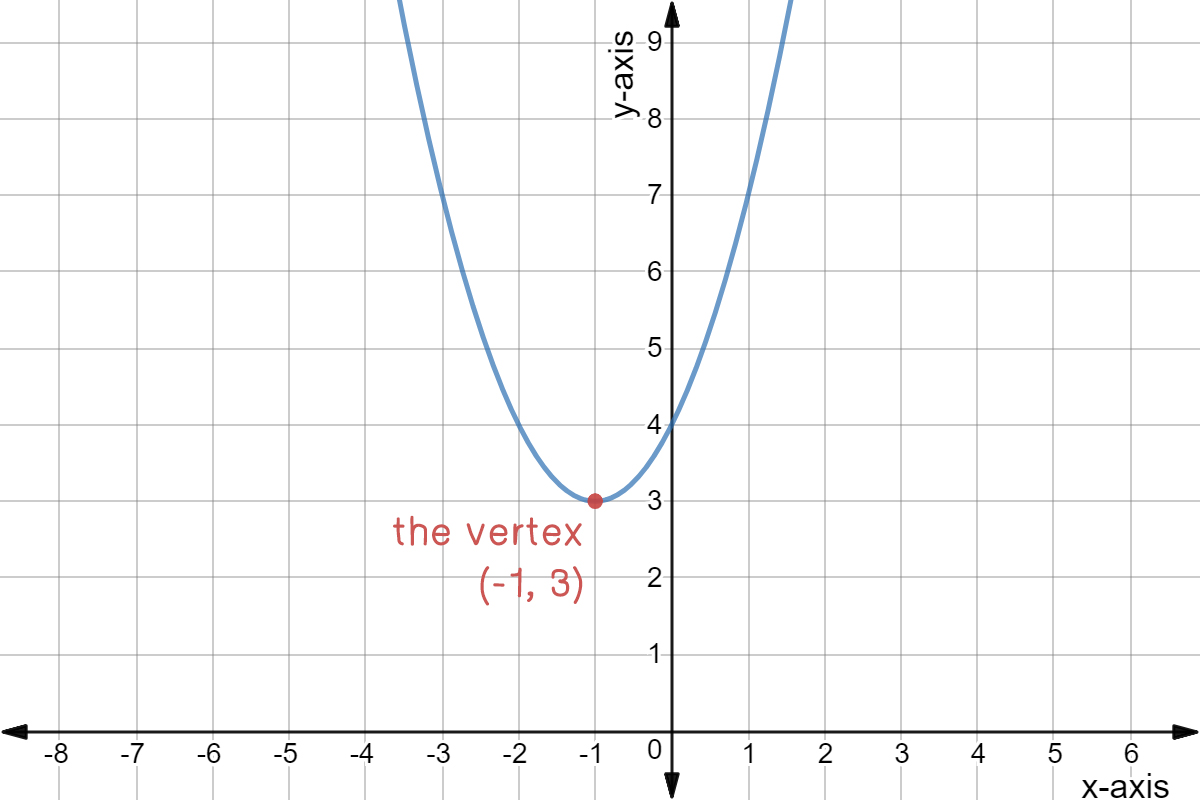



Intro To Quadratic Graphs Key Features Of Parabolas Expii




Graph Y X 2 Study Com




Quadratic Function
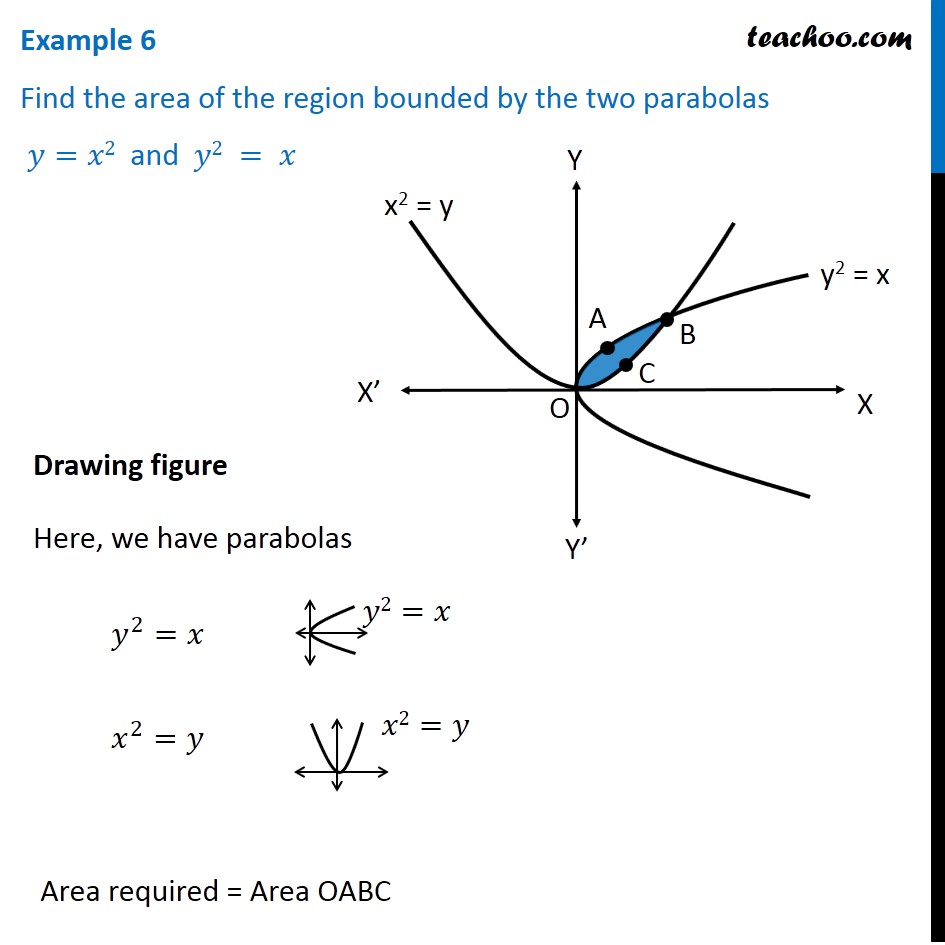



Example 6 Find Area Bounded By Two Parabolas Y X2 Y2 X



Graphing Quadratic Functions




Draw The Graph Of Y X 2 And Y X 2 And Hence Solve The Equation X 2 X 2 0




Quadratic Function



Quadratics Graphing Parabolas Sparknotes



Draw The Graph Of Y X 2 3x 4 And Hence Use It To Solve X 2 3x 4 0 Y 2 X 3x 4 Sarthaks Econnect Largest Online Education Community
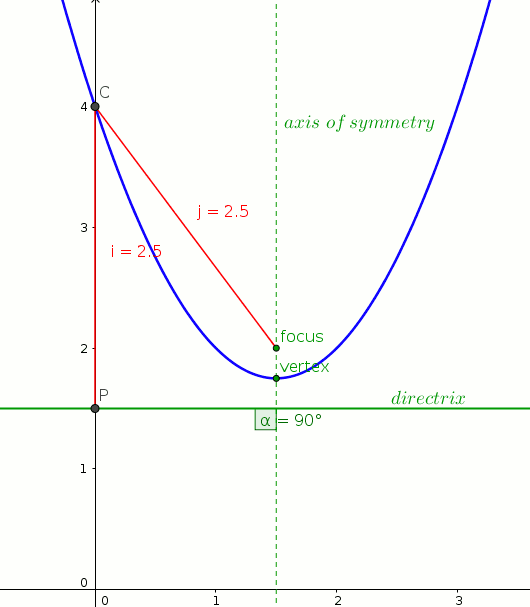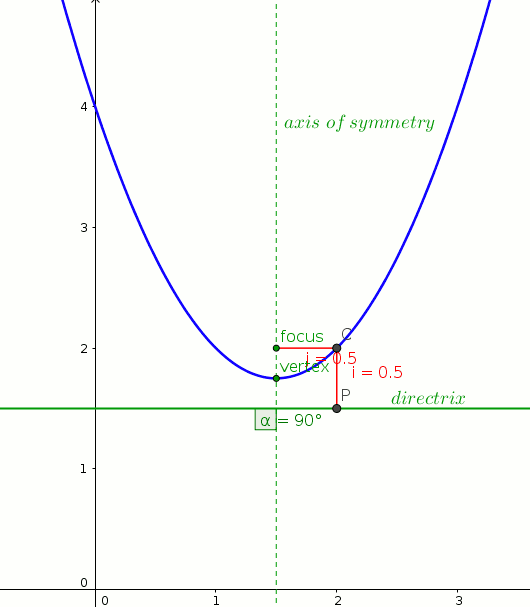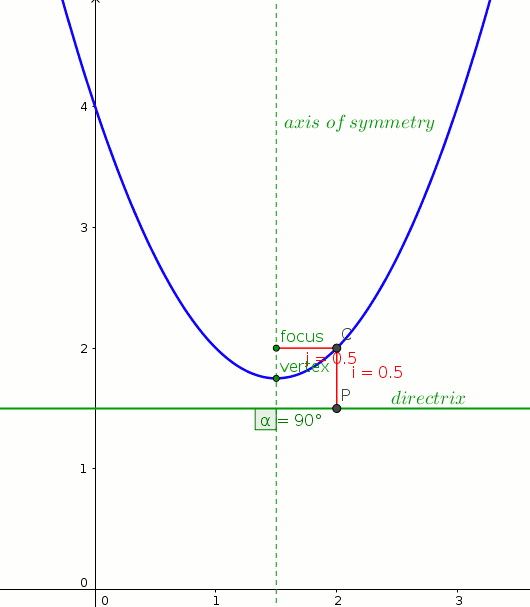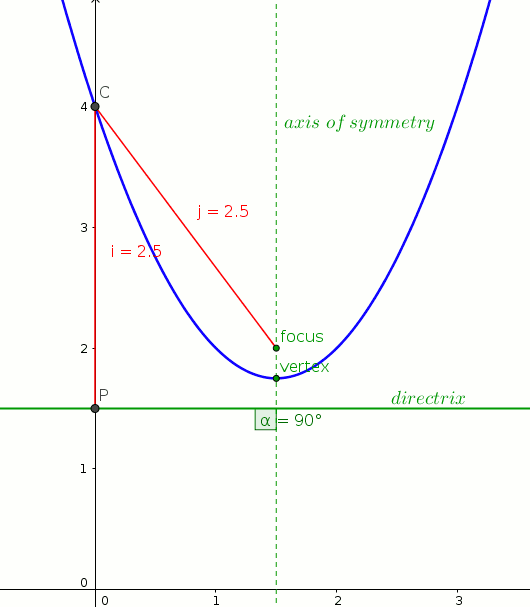



What Are The Vertex Focus And Directrix Of Y X 2 3x 4 Socratic




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram



1



Search Q Y 3d2 Graph Tbm Isch
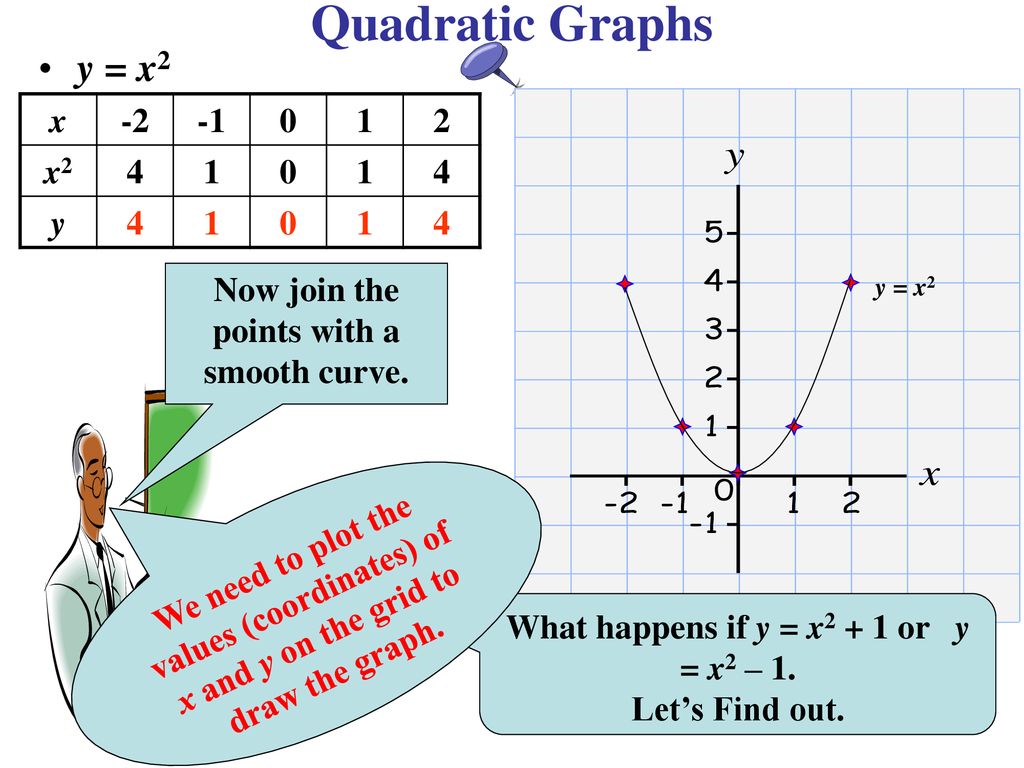



Quadratic Graphs Parabolas Ppt Download



Draw The Graph Of Y X 2 3x 2 And Use It To Solve X 2 2x 1 0 Sarthaks Econnect Largest Online Education Community
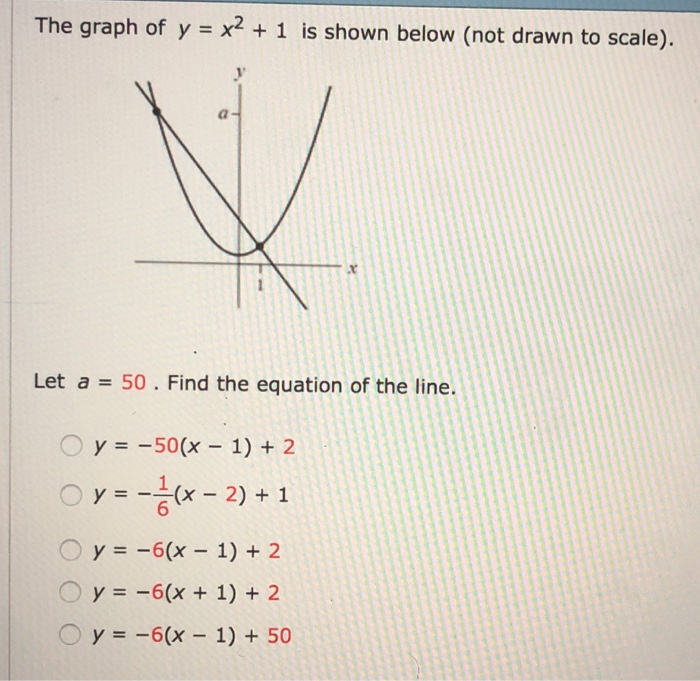



The Graph Of Y X2 1 Is Shown Below Not Drawn To Chegg Com



Graphing Quadratic Functions



Sketch The Parabola Of Equation Y X 2 6x 9 And Indicate Its Vertex Study Com



Graph The Parabola Y X 2 6x Mathskey Com
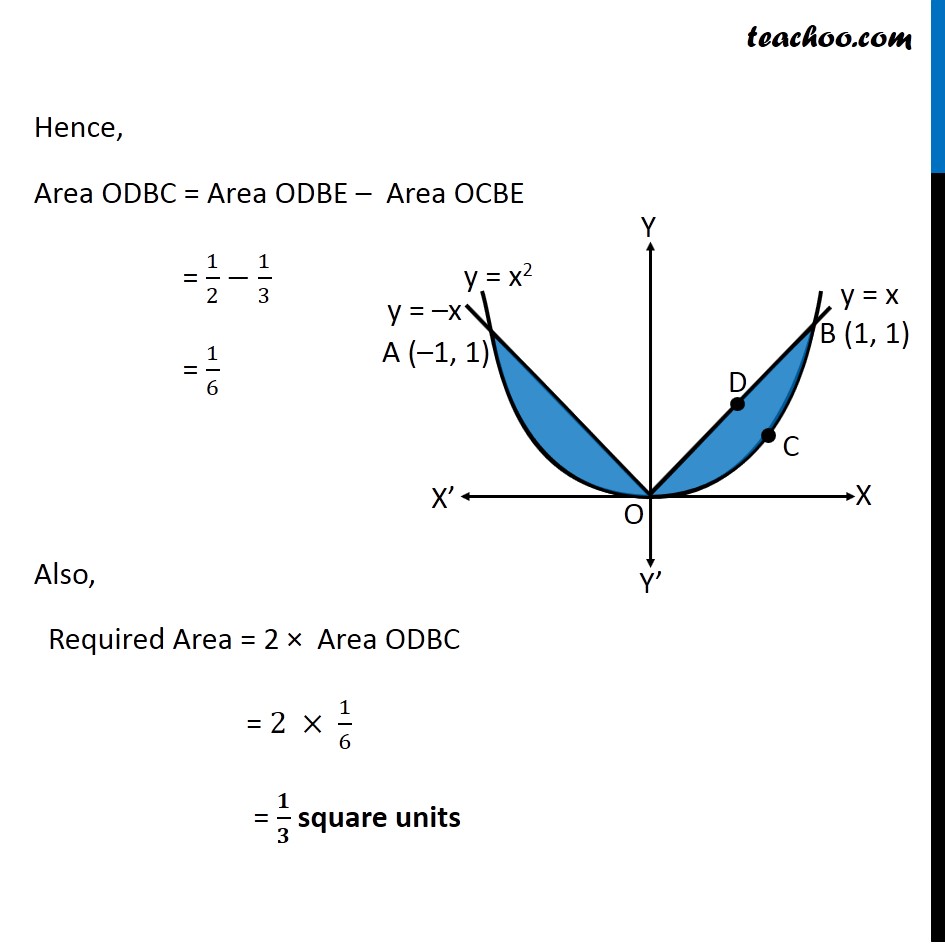



Misc 12 Find Area X Y Y X2 And Y X Class 12




Graphing Y X 2 6x Youtube



How To Graph Y X 2 1 Youtube



Graphing Quadratic Functions




Parabola Parent Function Mathbitsnotebook A1 Ccss Math




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram




How To Draw Y 2 X 2



0 件のコメント:
コメントを投稿