Algebra Q&A Library Q3) Use the inner product < p,q >= a,bo a,b¡ a,b2 to find < p, q >, p, d(p, q), and then find the angle between them for the polynomials in P2 if p(x) = 1 – x x², and q Explanation Since the given vectors are P and Q Also it is given that the angle between the vectors P and Q is = ∴PQ = Also P Q = Since , it is given that PQ = PQ , so we have Or , Or , Or , 4PQcos = 0 Find the angle between two vectors p and q, if p x q = pq Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow , the largest, most trusted online community for developers

Find The Angle Between Two Vectors P Vector And Q Vector If Resultant Of The Vector Is Given By R 2 Brainly In
If p+q=p-q then angle between p and q is
If p+q=p-q then angle between p and q is- Let the angle between two vectors P and Q be alpha and their resultant is R So we can write R^2=P^2Q^22PQcosalpha1 When Q is doubled then let the resultant vector be R_1, So we can write R_1^2=P^24Q^24PQcosalpha2 Again by the given condition R_1 is perpendicular to P So 4Q^2=P^2R_1^23 Combining 2 and 3 we get R_1^2=P^2P^2R_1^24PQcosalpha =>2PQcosalpha=P If p and q are statements then here are four compound statements made from them ¬ p , Not p (ie the negation of p ), p ∧ q, p and q, p ∨ q, p or q and p → q, If p then q Example 11 2 If p = "You eat your supper tonight" and q = "You get desert"



If Magnitude Of Vectors P And Q Are Equal Where P A B And Q A B Then What Is The Angle Between A And B Quora
We can nd a generating function F = F 1 (q;Q) by dividing the old variables p = m!cot(Q) (437) q This gives us @F 1 p= 1 F @qAnswer to What is the angle between the resultants of P Q and P Q where P and Q are two vectors By signing up, you'll get thousands of Example 7 AB is a linesegment P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see figure) Show that the line PQ is the perpendicular bisector of AB Given P is equidistant from points A & B PA = PB and Q is equidistant from points A & B QA = QB To prove PQ is perpendicular bisector
If p(x) and q(x) are arbitrary polynomials of degree at most 2, then the mapping < p,q >= p(2)q(2) p(0)q(0) p(2)q(2) defines an inner product in P3 Use this inner product to find < p,q >, llpll, llqll, and the angle tetha, between p(x) and q(x) for p(x) = 2x^26x1 and q(x) = 3x^25x6 < p;q >= ? Magnitude Sum of Two vectors Vector P and Vector q is given by r^2 =p^2q^22pqcos($) _____(i) here $ indicates angle between them We are given r=pq so Squaring both the sides we get r^2=p^2q^22pq _____(ii) From (i) and (ii) we can write p^2q^22pqcos($)=p^2q^22pq therefore 2pq=2pqcos($)Transcribed Image Textfrom this Question If p (x) and q (x) are arbitrary polynomials of degree at most 2, then the mapping < pq >= p (2)q (2) p (0)q (0) p (1)q (1) defines an inner product in P3 Use this inner product to find < p q >, p, q, and the angle theta between p (x) and q (x) for p (x) = 2x2 3x 1 and q (x) = 3x2
A tetrahedron has vertices P(1, 2, 1), Q(2, 1, 3), R(1, 1, 2) and O(0, 0, 0) The angle between the (7/31) (3) cos1(17/31) (4) cos1(19/35) Let the angle between P & Q is θ So, R=P2Q22PQ cos θ−−−−−−−−−−−−−−−−−−√⇒P2=P2Q22PQ cos θ⇒Q22PQ cos θ=0⇒Q2P cos θ=0⇒2P cos θ=−Q Given that R is perpendicular to P Therefore,Originally Answered What is the angle between p × q and q × p vectors?



Www Assignmentexpert Com Homework Answers Physics Answer Pdf




Given That P Q R If Pvector Qvector Rvector Then The Angle Between Pvector And Rvector Is 81 If Pvector Qvector Rvector 0 The The Angle Between Pvector And Rvector Is What Is The Relation Between 81
The angle between two vectors of magnitudes 12 N and 3N on a body is 60$^\circ$ the resultant w rt 12 N force is about 3 $\overrightarrow{a},\overrightarrow {b},\overrightarrow {c}$ are three consecutive vectors forming a triangle, then $\overrightarrow{a} \overrightarrow{b} \overrightarrow {c}$ is equal to Given PQ=R and P=Q=R When PQ=R or P R = Q (P R) (P R) = ( Q) ( Q) P2R22PR cos o1° (teta)=Q2 Coso1° = 1/2 (as P=Q=R) o1°=60° Therefore,angle between Pand Q is 60° I think my suggestions and knowledge may be helpful to us to u Thank you!!!The PQ and PQ are its diagonals Unless you know the lengths of the sides, we cannot proceed Note that if P and Q have equal magnitudes, the parallelogram is a rhombus, in which case the angle between the diagonals is 90 Given that (P vector Q vector) = (P vector Q vector)
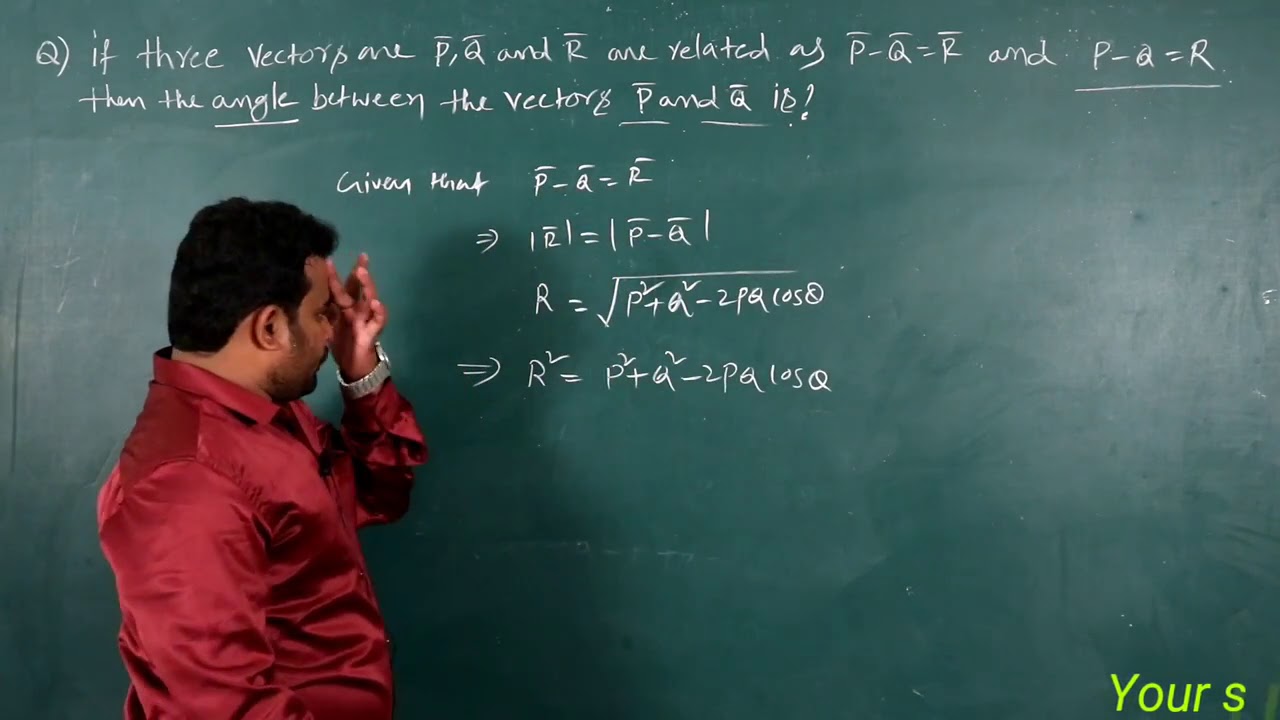



If P Q R Then Angle Between P Q Is Youtube




15 Two Forces P And Q Are In Ratio P Q 1 2 Iftheir Resultant I
4 p ˉ − 2 q ˉ are pairs of mutually perpendicular vectors then s i n (θ) is (θ is the angle between p ˉ and q ˉ ) Hard View solutionLet R be the resultant vector So, R = (P Q )(P − Q )= 2P Thus R is in same direction along P with twice its magnitude Hence, angle between them is zero Answer verified by TopprOver a field of characteristic 2, the two vectors can only be equal for all vectors p, q (and even defining the angle is a bit tricky) In any other field, q = 0 , and there is no welldefined angle with a null vector, even if there is for other vectors




At What Angle Two Forces P Q And P Q Act So That Resultant Is I Sqrt 2 P 2 Q 2 Ii Sqrt 2 P 2 Q 2 Iii Sqrt 2 P 2 Q 2




Q7 In Triangle Pqr Angle Q 90 Lido
If P, Q and R are three points on a line and Q is between P and R,then prove that PR QR= PQ asked in Class IX Maths by aditya23 ( 2,134 points) introduction to euclid's geometryP is called the hypothesis and q is called the conclusion For instance, consider the two following statements If Sally passes the exam, then she will get the job If 144 is divisible by 12, 144 is divisible by 3About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators




Q 57 2j 3k 57 Pq Then Angle And Is 2 300 3 450 4 600 If Physics Motion In A Straight Line Meritnation Com



The Resultant Of Two Forces P And Q Is R If Q Is Doubled The New Resultant Is Perpendicular To P How Can I Prove Q R Quora
In triangle law head of vector P is connected to tail of vector Q But angle between two vectors is possible tail to tail Hence shift Vector Q from head of vector P to tail of vector P without changing direction and keeping the shift parallel This way we get the angle between vector P and Vector QSolution for a) Find < p, q>, \pl, d (p, q), and then find the angle between them for the polynomials in P2 if p(x) =3x² 2x – 5 , and q(x)= x5x? R P 2 Q 2 2PQ cosα From the above equation it is evident that R depends on the angle between P and Q ie on α Resultant of two forces P and Q is R R P Q Square of Resultant R is R2 P2 Q2 2PQ cos α α is the angle between P and Q Then the magnitude of R is equal to R p 2 Q 2 2 P Q And the angle is 90 degree Hope that helps you




Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube




The Resultant Of Two Forces P And Q Is Of Magnitude P If The Force P Is Doubled Q Remainin Youtube
5 p ˉ − 3 q ˉ and 2 p ˉ q ˉ ; what is the angle between (PQ) and (P*Q) Share with your friends Share 13 90 degree Since PQ will be in the same plane as P and Q and P × Q will be Find the magnitude and direction of the resultant of two forces p and Q in terms of their magnitudes and angle Q between them asked in Physics by Rohit01 (546k points) motion in a plane;




8 If P And Q Are Two Unit Vectors And The Angle Between Them Is 60 Then Is 1 2 P Q D2 1 2




The Resultant Vec P And Vec Q Is Perpendicular To Vec P What Is The Angle Between Vec P And Vec Q
Then there is a mathematical relationship between the real power (P), and the reactive power (Q), called the complex power The product of the rms voltage, V applied to an AC circuit and the rms current, I flowing into that circuit is called the "voltampere product" (VA) given the symbol S and whose magnitude is known generally as apparentLlqll= ?plz show workLogically they are different In the first (only if), there exists exactly one condition, Q, that will produce P If the antecedent Q is denied (notQ), then notP immediately follows In the second, the restriction on conditions is gone The usual rules apply, and nothing follows from denying the antecedent Q Share Improve this answer




If Vector P Q Pq Then Angel Between P And Q Brainly In



Two Vectors P And Q Are Inclined Towards Each Other At An Angle Theta What Is The Unit Vector Perpendicular To The P Vector And The Q Vector Quora
Three forces P, Q and R are acting at a point in a plain The angle between P Q and Q R are 1500 10 respectively, then for equilibrium, forces P,Q R are in the which ratio Physics Motion In A Plane p != q implies that p is not equal to q !(p==q) implies first execution of statement p==q and then the negation of the boolean value return after execution of first statement Suppose p = 5 and q = 5 1> p != q In this case, result of execution of the statement will be false 2>They are antiparallel by definition, so the answer is 180 degree or radians They are antiparallel by definition, so the answer is 180 degree or radians



1




Given P Q R If Vector P Vector Q Vector R Then The Angle Between Vector P And Q Is Theeta1 If Vector Brainly In
If PQ = PQ, then angle between P and Q is Get the answer to this question and access more number of related questions that are tailored for studentsAngle will be zero because resultant of PQ and PQ is 2P and which is parallel to P itselfExample 213 p_q!r Discussion One of the important techniques used in proving theorems is to replace, or sub However, if pis true and qis false, then p^qwill be true Hence this case is not possible Case 2 Suppose (p!q) is false and p^qis true p^qis true only if pis true and qis false But in this case, (p!q) will be true So




Two Forces P And Q Are In Ratio P Q 1 2 If Their Resultant Is At An Angle Tan 1 Sqrt3 2 To Vector P Then Angle Between P And Q Is




If P Q P Q Then
Given that P 12, Q = 5 and R = 13 also PQ=R, then the angle between P and Q will be9 INNERPRODUCT 2 Angle The angle θ between two vectors xand y is related to the dot product by the formula xT y= kxkkykcosθ 911 Example Find the angle between x= 2,−3T and y= 3,2T Solution We solve the equation above to getThe angle between two vectors of magnitudes 12 N and 3N on a body is 60$^\circ$ the resultant w rt 12 N force is about 3 $\overrightarrow{a},\overrightarrow {b},\overrightarrow {c}$ are three consecutive vectors forming a triangle, then $\overrightarrow{a} \overrightarrow{b} \overrightarrow {c}$ is equal to




In Given Figure Pqr Is A Right Angled Triangle Right Angled At Q And Qs Bot Pr Youtube



How To Prove That Non Zero Vectors P Q P Q If They Re Perpendicular Quora
0 votes 1 answer Two equal forces are acting at a point and angle between them in 60° Calculate magnitude of Resultant of theseTwo forces P and Q are acting at a particle The angle between the forces is θ and the resultant of the forces is R If the resolved part of R in the direction of P is 2P Resolved part of R = Q cosθ P ie 2P = Q cosθ P P = Q cosθ Download Question With Solution PDF ›› Transcript Example 5 In Δ OPQ, rightangled at P, OP = 7 cm and OQ – PQ = 1 cm (see Fig) Determine the values of sin Q and cos Q In is given that in triangle OPQ, OQ – PQ = 1 cm OQ = 1 PQ Using Pythagoras theorem (Hypotenuse)2 = (Height)2 (Base)2 OQ2 = PQ2 OP2 (1 PQ)2 = PQ2 (7)2 1 PQ2 2PQ = PQ2 49 1 PQ2 2PQ – PQ2 – 49 = 0 2PQ – 48 = 0 2PQ




If P Q Pq Then Angle Between P And Q Is



Search Q Unit Vector Formula Tbm Isch
If a parallelogram is constructed on the vectors apqbpqandpqa¯=3p¯q¯,b¯=p¯3q¯andp¯=q¯=2 and angle between pandqp¯andq¯ is π3, and angle between lengths of the sides is 713In conditional statements, "If p then q" is denoted symbolically by "p q"; Explanation Given, → P → Q = → R So, we can write, ∣∣ ∣→ R ∣∣ ∣ = √P 2 Q2 2P Qcosθ ,where θ is the angle between the two vectors Or, R2 = P 2 Q2 2P Qcosθ Given, P 2 Q2 = R2 So, R2 = R2 2P Qcosθ Or, 2P Qcosθ = 0




Given That P Q R If P Q R Then The Angle Between P And R Is Theta1 If P Q 0 Then The Angle Physics Physics And Mathematics Meritnation Com




If P Vector Dot Q Vector Is Equal To Pq Then Angle Between P And Q Is Brainly In
If the vectors 3 p ˉ q ˉ ;(435) so the new momentum E P= (436) 2 is just proportional to the energy, while Qis a cyclic variable Is this transformation canonical?(1)theta1=theta2 (2)theta1=theta2/2 (3)theta1=2theta2 (4)none of these



If Vector P Q Pq Then The Angles Between Vector P And Vector Q Is Sarthaks Econnect Largest Online Education Community




Given That P Q R If Vec P Vec Q Vec R Then The Angle Between Vec P And V Youtube
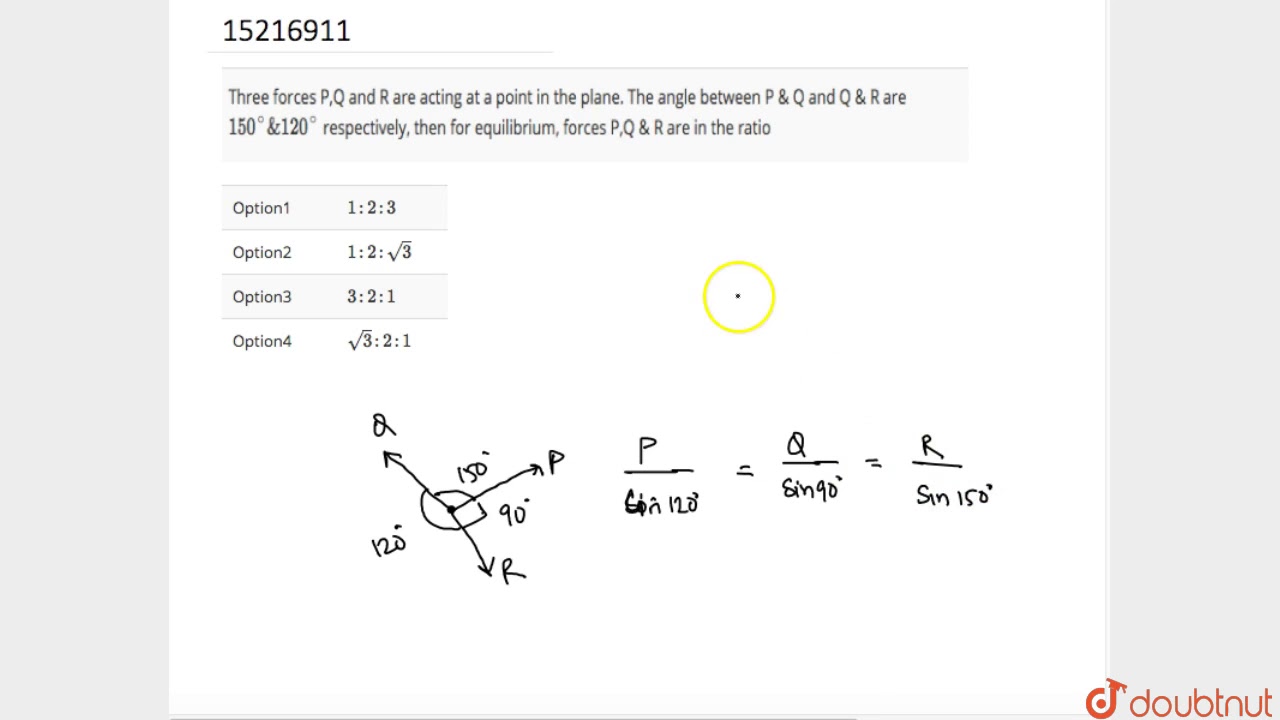
The resultant of two vectors and is If is doubled then the new resultant vector is perpendicular to Then magnitude of is 599k 2907k 236 Two vectors are added, the magnitude of resultant is 15 units If is reversed and added toClearly, the angle between P and R is 360 o – (150 o 1 o) = 90 o By Lami's theorem, P / sin 1 o = Q / sin 90 o = R / sin 150 o P / (√3 / 2) = Q / 1 = R / (1 / 2) P / √3 = Q / 2 = R / 1 Forces P, Q, R are in the ration √3 2 12mPsin(Q) for constant Then K= H= P 2 cos (Q) sin2(Q) = P 2;




If P Q P Q What Is The Angle Between The P Vector And Q Vector Quora



If Magnitude Of Vectors P And Q Are Equal Where P A B And Q A B Then What Is The Angle Between A And B Quora
If we call the first part p and the second part q then we know that p results in q This means that if p is true then q will also be true This is called the law of detachment and is noted $$\left (p \to q)\wedge p \right \to q$$ The law of syllogism tells us that if p → q and q → r then p → r is also true This is notedQuestion From – DC Pandey PHYSICS Class 11 Chapter 05 Question – 043 VECTORS CBSE, RBSE, UP, MP, BIHAR BOARDQUESTION TEXTThe angles between PQ and PQ wilIf a force (F) is acting on a rigid body at any point P, then this force (F) can be replaced by Q5 The radius of arc is measured by allowing a mm diameter roller to oscillate to and fro on it and the time for 25 oscillations is noted at 5625 s




Find The Angle Between Two Vectors P Vector And Q Vector If Resultant Of The Vector Is Given By R 2 Brainly In




The Resultant Of Two Vectors Vec P And Vec Q Is Vec R If The Magnitude Of Vec Q Is Youtube



Three Forces P Q And R Are Acting At A Point In The Plane The Angle Between Youtube




C 45 Q 25 If P Q Pq Then Angle Between Phu Q 15 B 30



12 3 The Dot Product Ppt Download



Angle Between Vector P Q P Q Wil Be




Two Forces P And Q Are In Ratio P Q 1 2 If Their Resultant Is




Two Forces P And Q Have A Resultant Perpendicular To P The Angle Between The Forces Is Quora




If Vector P Q And R Have Magnitude 5 12 And 13 Units And Vec P Vec Q Vec R The Angle Between Q And R Is




If Vecp Vecq Pq Then Angle Between Vecp And Vecq Is



Two Forces P 1 Dyn Q 3 Dyn And They Are In 90 Degree To Each Other What Is The Angle Between The Vectors P Q And P Q Physics Topperlearning Com




If P Q P Q What Is The Angle Between The P Vector And Q Vector Quora



2




The Angles Between P Q And P Q Will Be Youtube




Find Angle Between P Vector And Q Vector If Resultant Is Given By R 2 P 2 Q 2 Physics Topperlearning Com 40y2cnxx
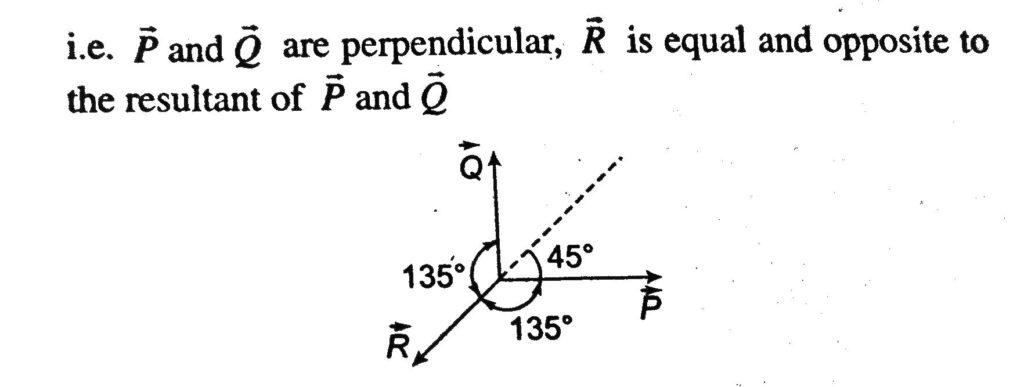



Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And




Given That P Q R If P Q R Then The Angle Between P And R Is Theta1 If P Q R 0
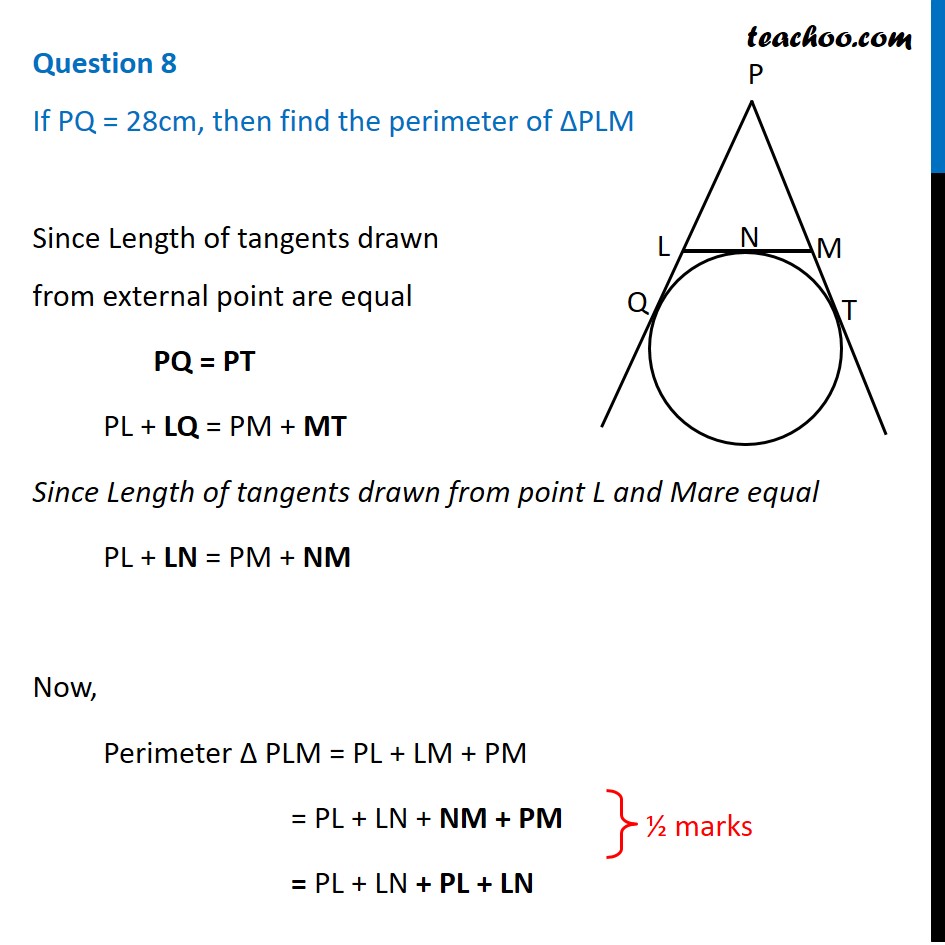



If Pq 28cm Then Find The Perimeter Of Plm Cbse Class 10 Sample Pap



The Resultant Of The Vector P And Q Is Perpendicular To The Vector P What Is The Angle Between P And Q Quora




What Is Angle Between P Q And P Cross Q Brainly In




Find The Unit Vector In The Direction Of Pq Vector Where P And Q Are The Points 1 2 3 And 4 5 6 Youtube




If P Q P Q And O Is The Angle Between P And Q Then A 0 00 B 0 900 C P 0




Three Forces P Q And R Are Acting On A Particel In The Plane The Angle Between P Youtube




If P Q R And P Q R The Ratio Of Angles Between P Amp R To P Amp Q Is Brainly In




What Is The Angle Between P Q And P Q Youtube




Points P Q R And S Are Collinear Point Q Is Between P And R R Is Between Q And S And Pq Rs If Ps 22 And Pr 18 What Is The Value Of




Given That P Is Equal To Q Is Equal To R E P Vector B Vector Is Equal To R Vector Then The Angle Brainly In




The Angle Between P Q And P Q Will Be 1 90 2 Between 0 And 180 3 180 Only 4 None Of These Pt If The



Ty6bmbei8scu2m



Wacfxpebpfijbm



Www Usna Edu Users Oceano Raylee Sm223 Ch12 3 Stewart 16 Pdf




9 Given That P Q And That Is Perpendicular To If P R Then




Given P Q R And That R Is Perpendicular To P If P R Then What Is The Angle Between P And Q Quora




The Resultant Of Two Vectors P And Q Is R If Q Is Doubled T Scholr



Q Tbn And9gcsixghtqlhknrjicxvapffrgivqgajj4gixt5fb6tnm7o5xirwh Usqp Cau




Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And




Two Forces Of Magnitudes P Q And P Q Make An Angle 2ss With One Another And Their Resultant Makes An Brainly In



If P Dot Q Vector 0 And P Q Vector 0 Then What Is The Angle Between The Q And R Vector Quora
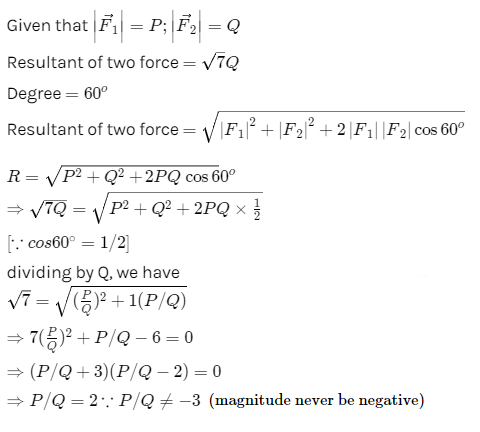



If The Resultant Of Two Forces Of Magnitudes P And Q Acting At A Poin Askiitians



Three Forces P Q And R Are Acting On A Particle In The Plane The Angle Between P And Q Q And R Are 150 And 1 Respectively Sarthaks Econnect




If Vector P Q And R Have Magnitude 5 12 And 13 Units And Youtube




If Vector P Vector Q P Q Then The Angle Between P And Q Is Maths Vector Algebra Meritnation Com




Two Forces P And Q Are In Ratio P Q 1 2 If Their Result Scholr



画像をダウンロード If P Qp Q Then ニスヌーピー 壁紙




If Angle Between 2 Vector P Vector And Q Vector Is 60 And Magnitude Of Resultant Of This Vector Is Brainly In




Example 27 If I J K 2i 5j 3i 2j 3k And I 6j K Are Position Vectors



What Is The Angle Between Vector P Q And Q P Quora



Www Hsn Uk Net Files Hsn




Defining The Angle Between Vectors Video Khan Academy




9 At What Angle Do The Two Forces P Q And P Q Act So That The Resultant Is 3p Q Ans 60




Engen1 B 11 09 18 Lecture Notes 29 Course Engen1b Date 11 Revision Of Matrix Algebra There Is Sample Test Sample Test Put Up On Moodle For Your Revision Studocu



Two Forces P And Q Have Their Resultant As R If P Is Increased The New Resultant Bisects The Angle Between R And P What Is The Increase In P Quora




The Angles Between P Q And P Q Will Be Youtube



Search Q Angle Between Two Vectors Tbm Isch



Web Auburn Edu Holmerr 2660 Textbook Innerproduct Print Pdf




Given P Q R If Vector P Vector Q Vector R Then The Angle Between Vector P And Q Is Theeta1 If Vector Brainly In




If Ab Qr Pr And Ca Pq Then Youtube




P Q R S Are Vector Of Equal Magnitude If P Q R 0 Angl Scholr




Two Forces P And Q Are In Ratio P Q 1 2 If Their Resultant Is At An Angle Tan 1 Sqrt3 2 Youtube




If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora




If Two Forces P And Q Are Such That P Q P Q Then What Is The Angle Between P And Q Quora



Http People Math Harvard Edu Knill Teaching Summer11 Handouts 14 Linesplanes Pdf




15 If Vectors P Q And R Have Magnitudes 5 12 And 13 Unit Scholr




If P Q Pq Then Angle Between P And Q Is




If P Q R And P Q Sqrt 3 And R 3 Then The Angle Between P And Q Is




162 9 Given That P 0 R And P2 Q2 R2 The Angle Between P And Q Is Donu 1 O 4 Tt



Www Usna Edu Users Oceano Raylee Sm223 Ch12 3 Stewart 16 Pdf



In Fig 8 9 O Is The Centre Of A Circle Pq Is A Chord And The Tangent Pr At P Makes An Angle Of 50degree With Pq Find Poq Sarthaks Econnect




Given That P Q R If P Q R Then The Angle Between P And R Is Theta1 If P Q 0 Then The Angle Physics Physics And Mathematics Meritnation Com




Two Forces Of Magnitudes P Q And P Q Make Equal Angle 2a With One Another Their Resultant Makes An Angle Physics Current Electricity Meritnation Com
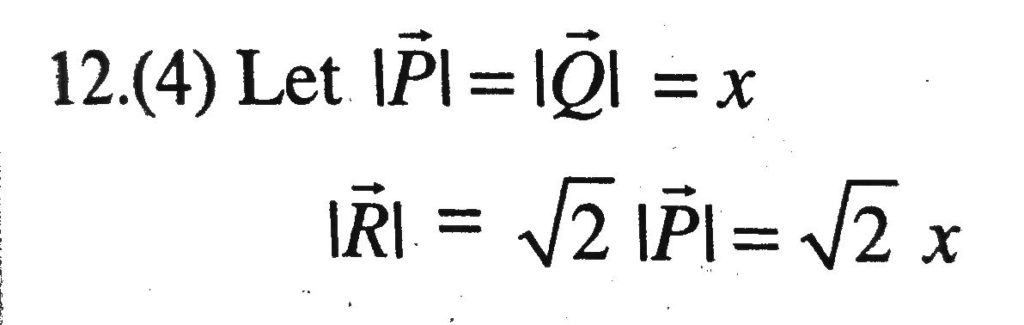



Three Vector P Q R Are Such That P Q R 2p And P Q R 0 The Angle Between P And Q Q And R And



What Is The Angle Between Vector P Q And Q P Quora




If Vectors P Q And R Have Magnitude 5 12 And 13 Units And Overrightarrow P Overrightarrow Q Overrightarrow R Then Angle Between Q And R Is Snapsolve



What Is The Angle Between P And The Cross Product Of P Q And P Q Quora



What Is The Angle Between Vector P Q And Q P Quora




What Is The Angle Between P And The Cross Product Of P Q And P Q



0 件のコメント:
コメントを投稿