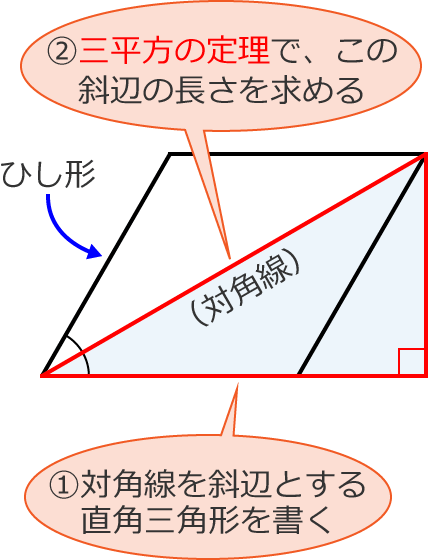
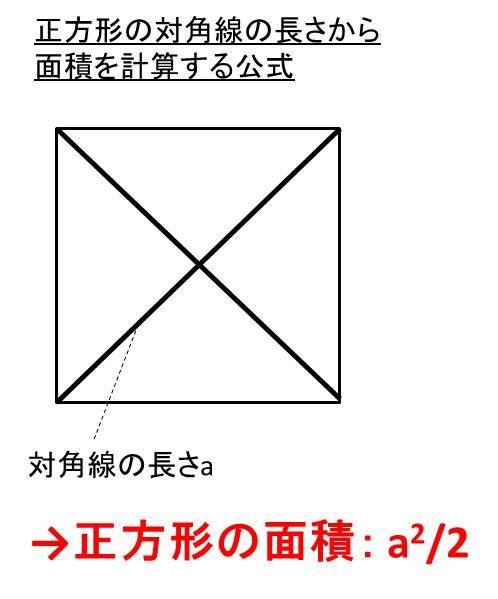
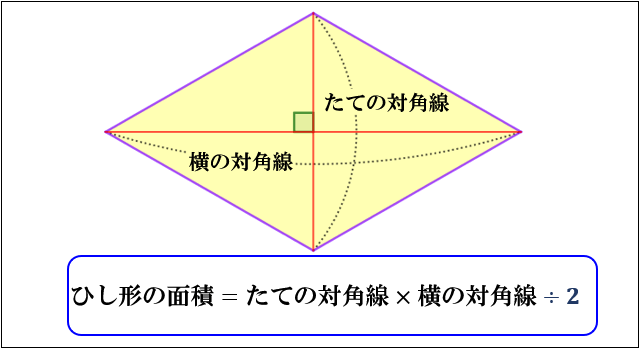
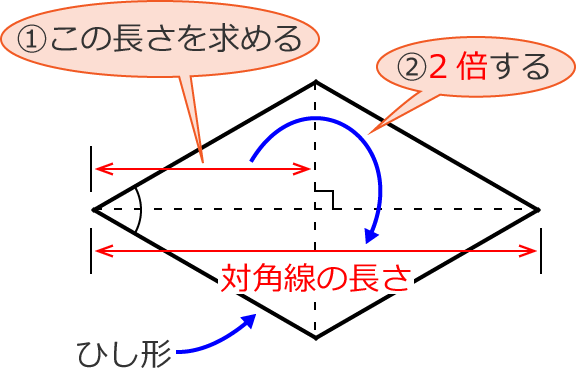
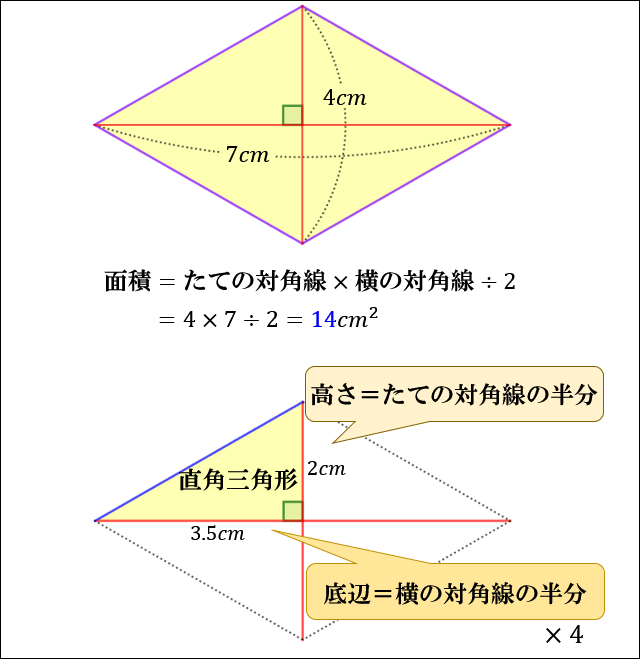
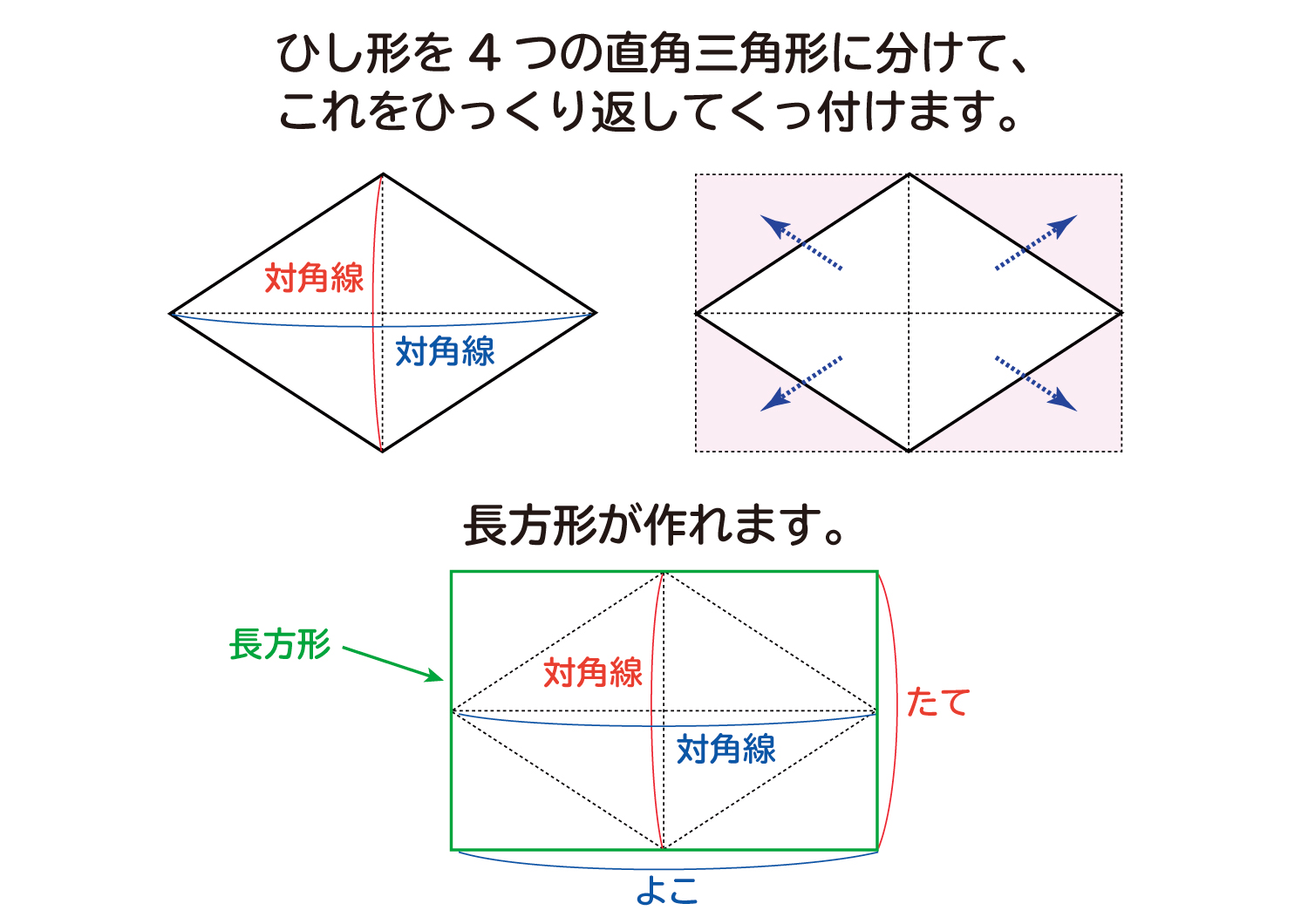
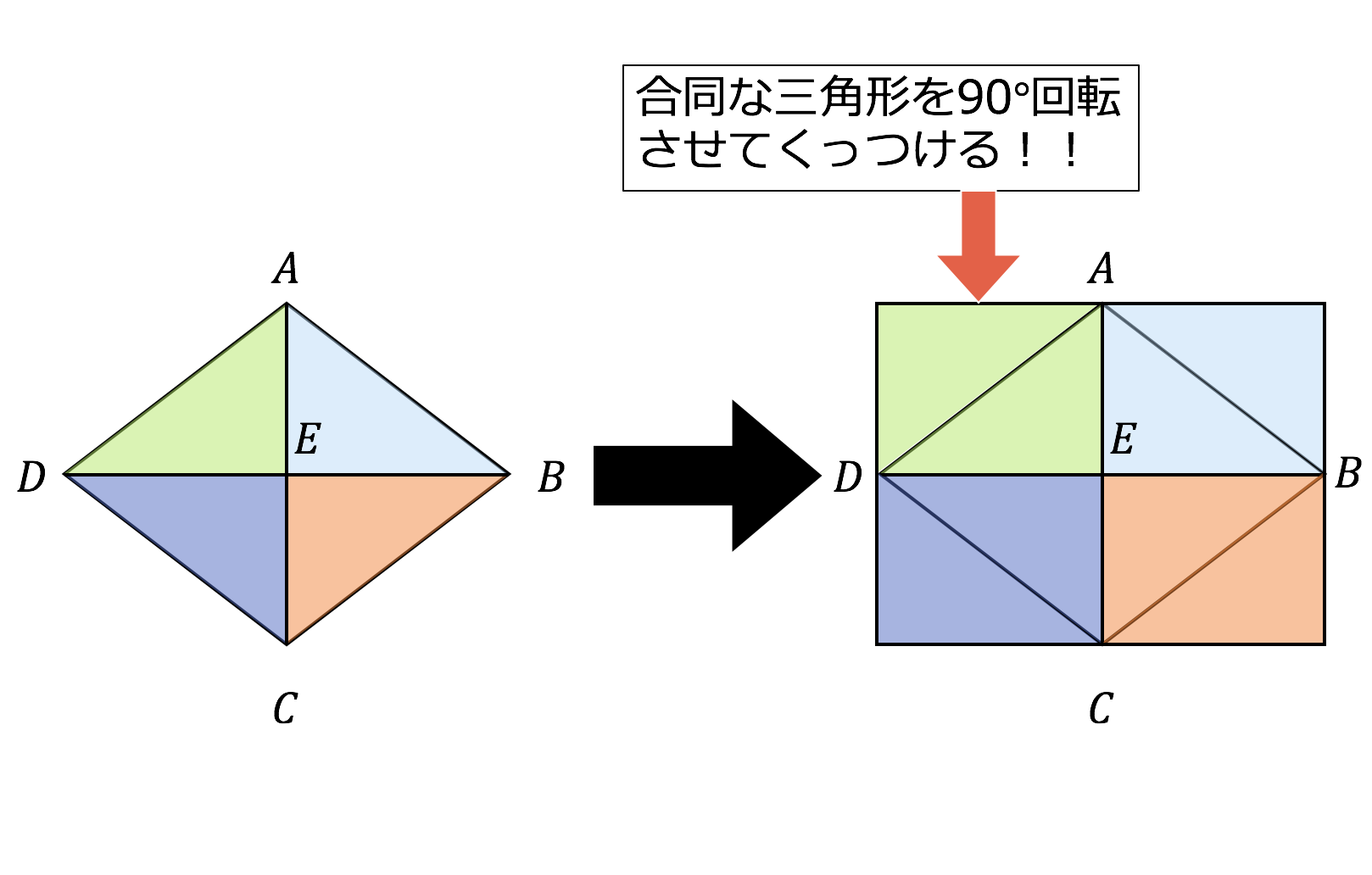
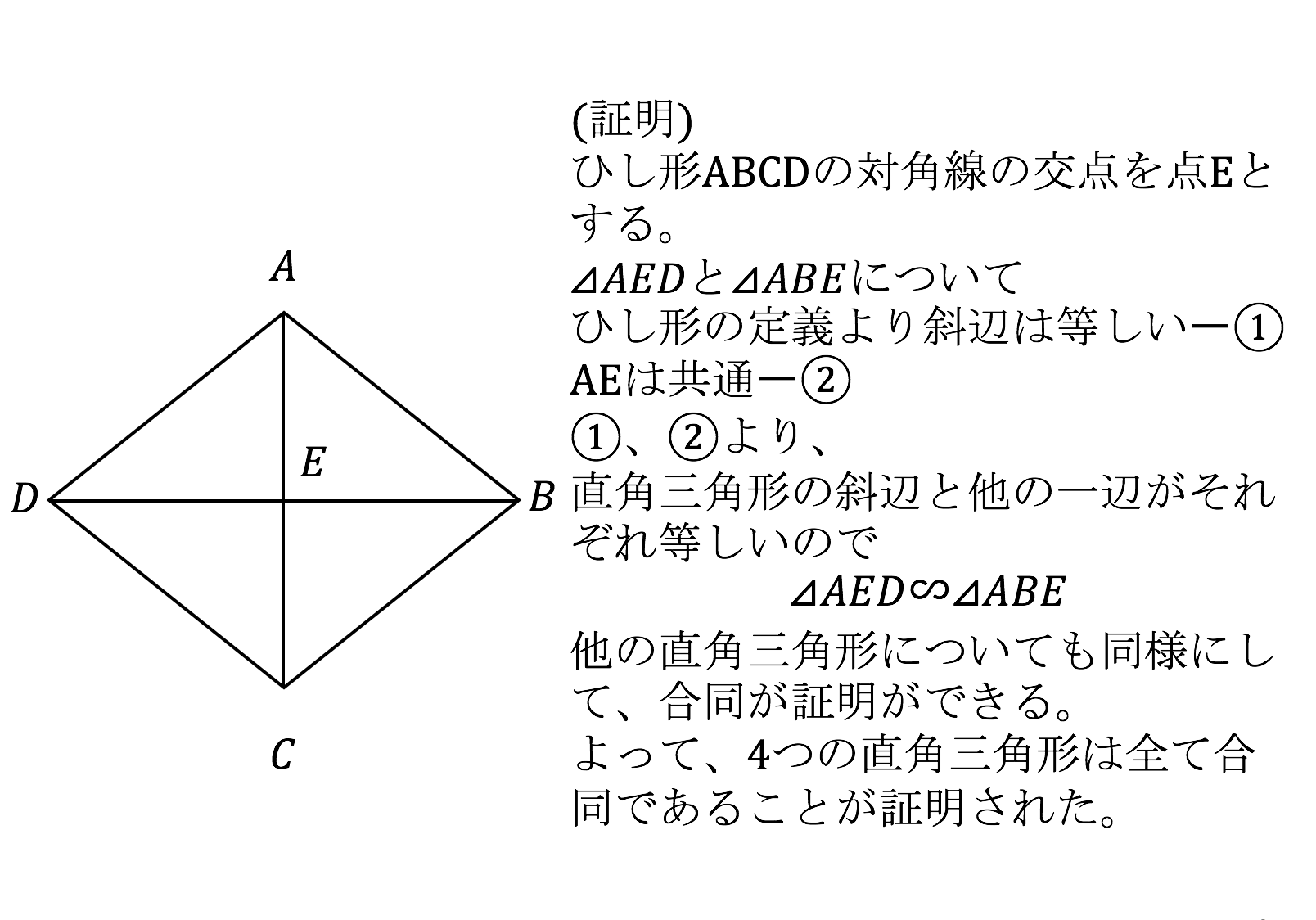
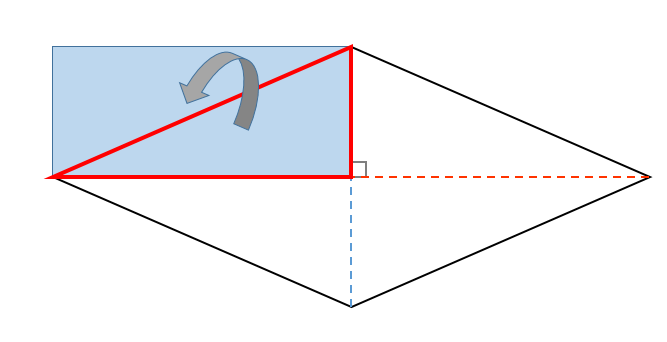
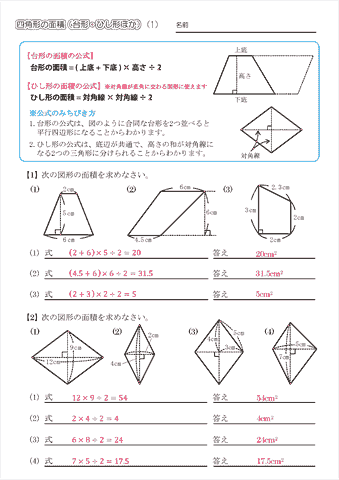
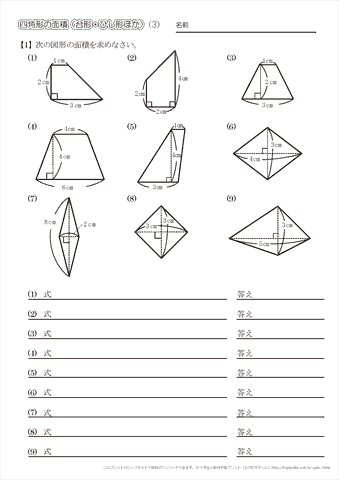
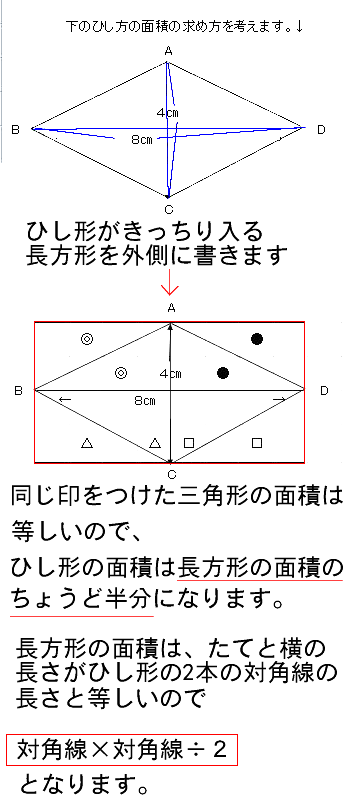
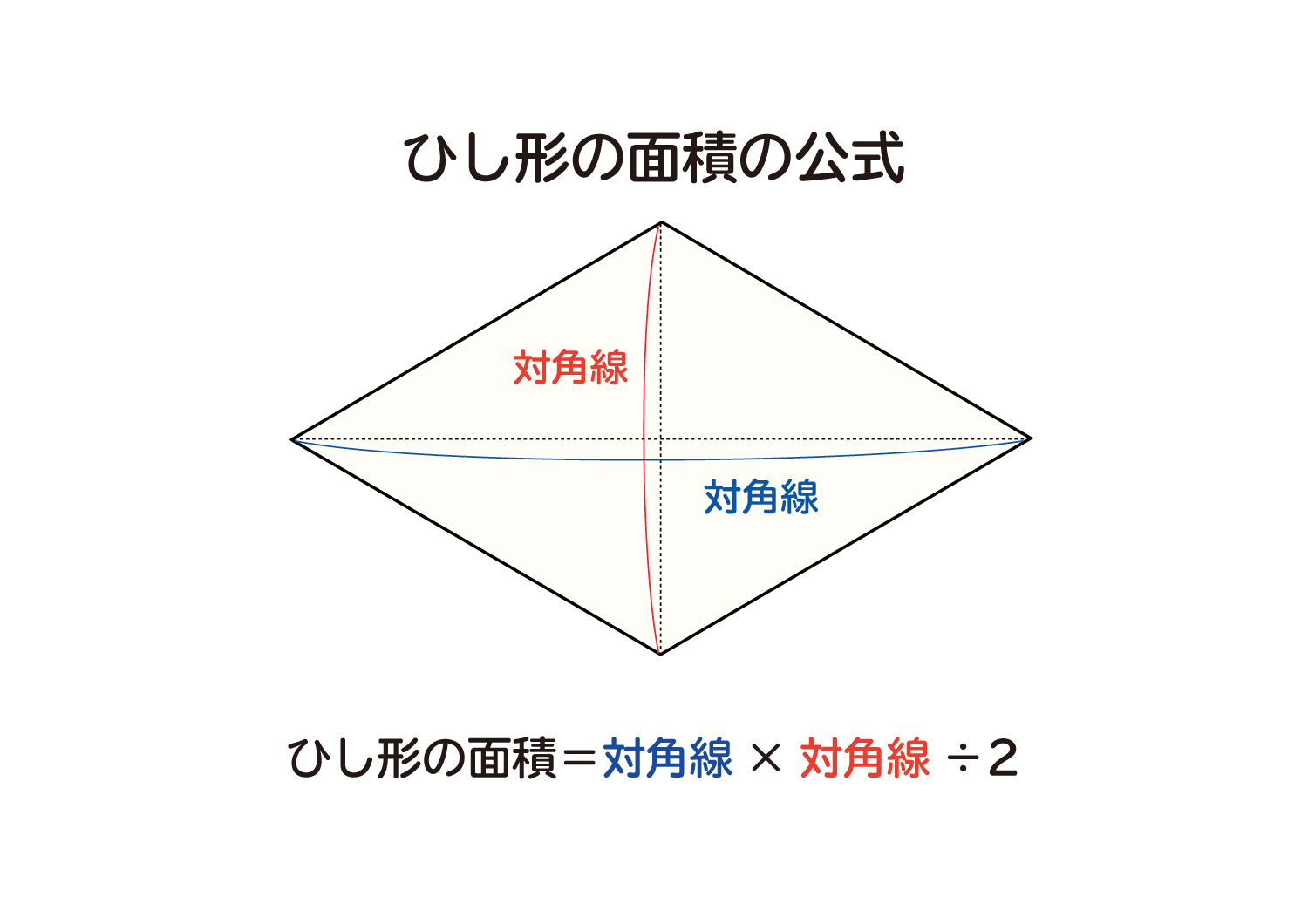
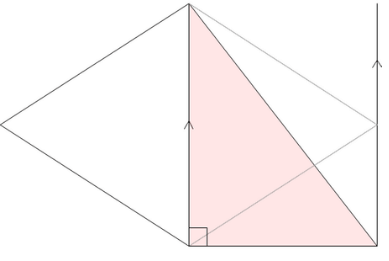
ひし形の面積は、この直角三角形の面積の4倍なので \(ひし形=直角三角形×4=(たて×横÷8)×4\) \(=たて×横÷2\) となり、ひし形の面積の公式が求まります。 ④ 台形の面積 台形の面積は、\(「面積=(上底下底)×高さ÷2」\) で求められます。
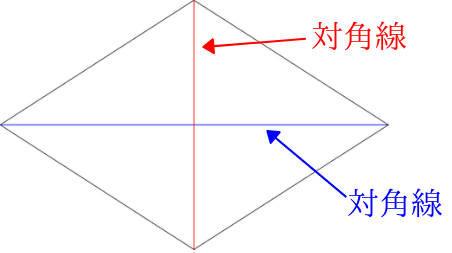
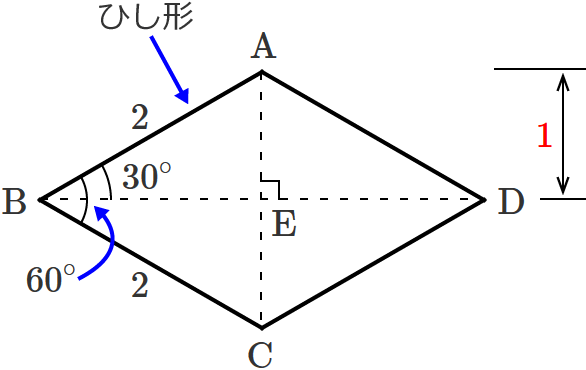
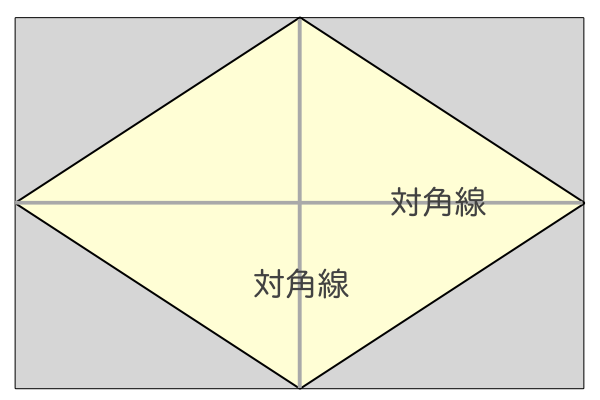
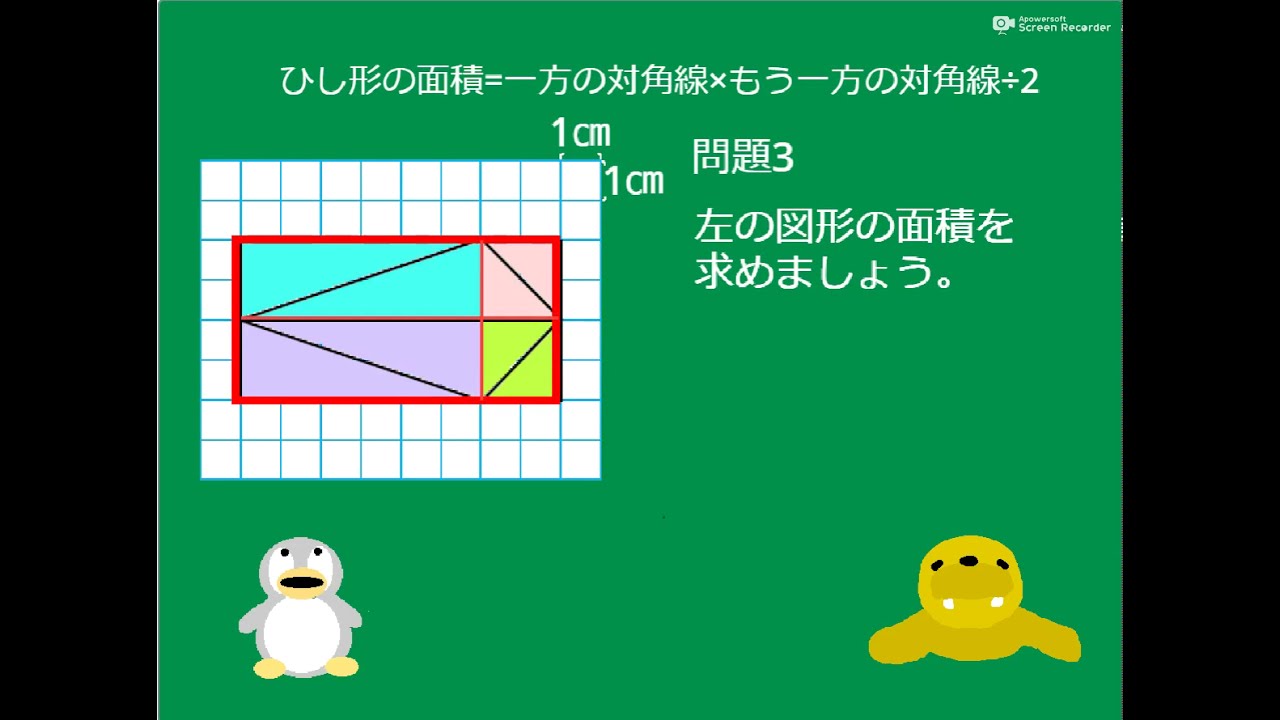
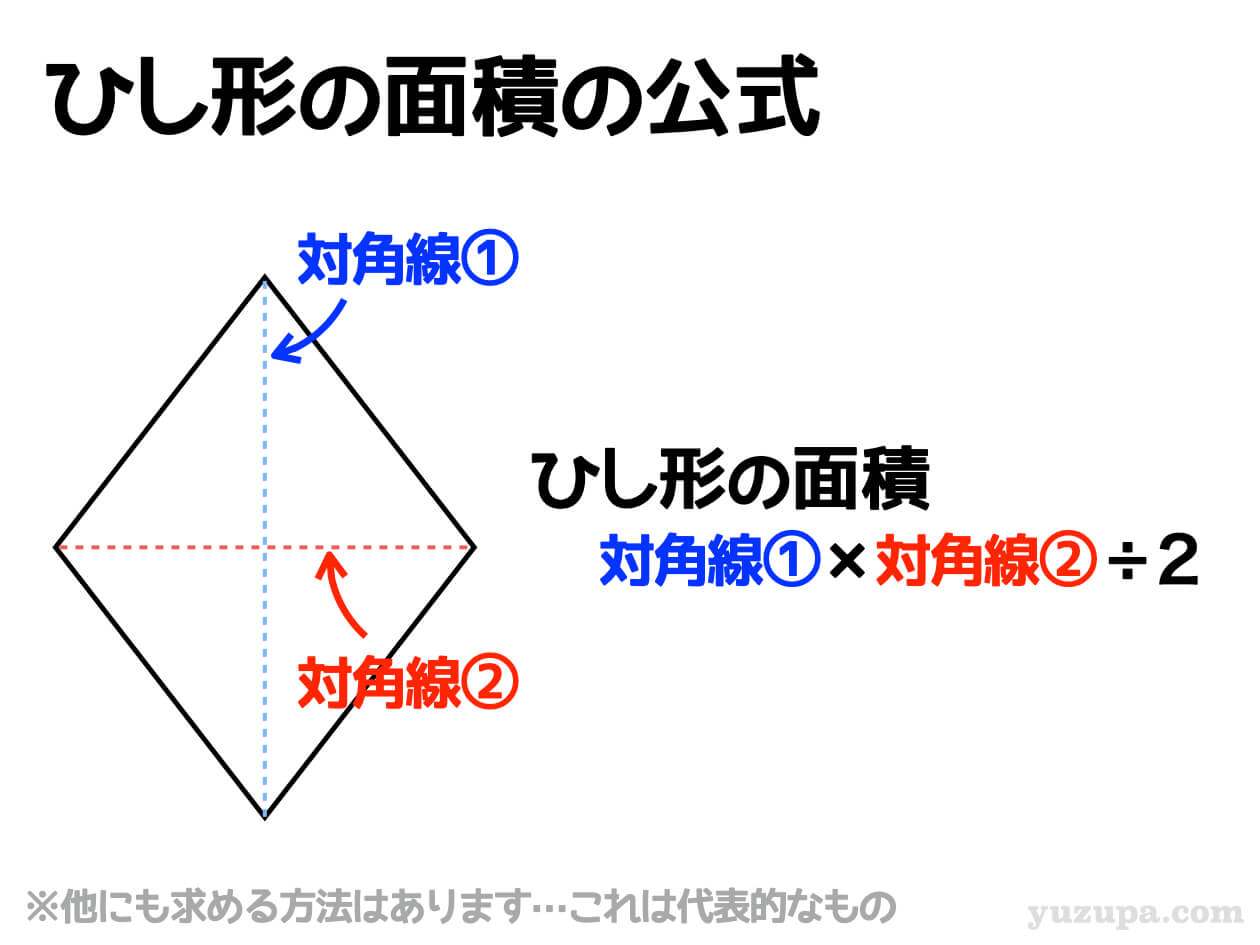
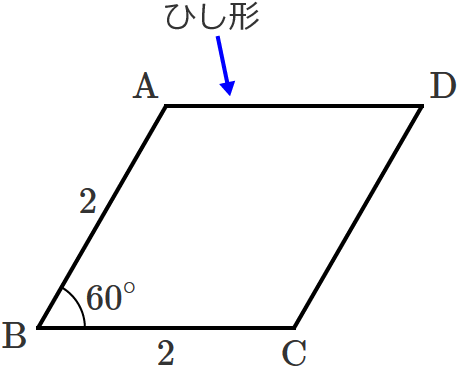
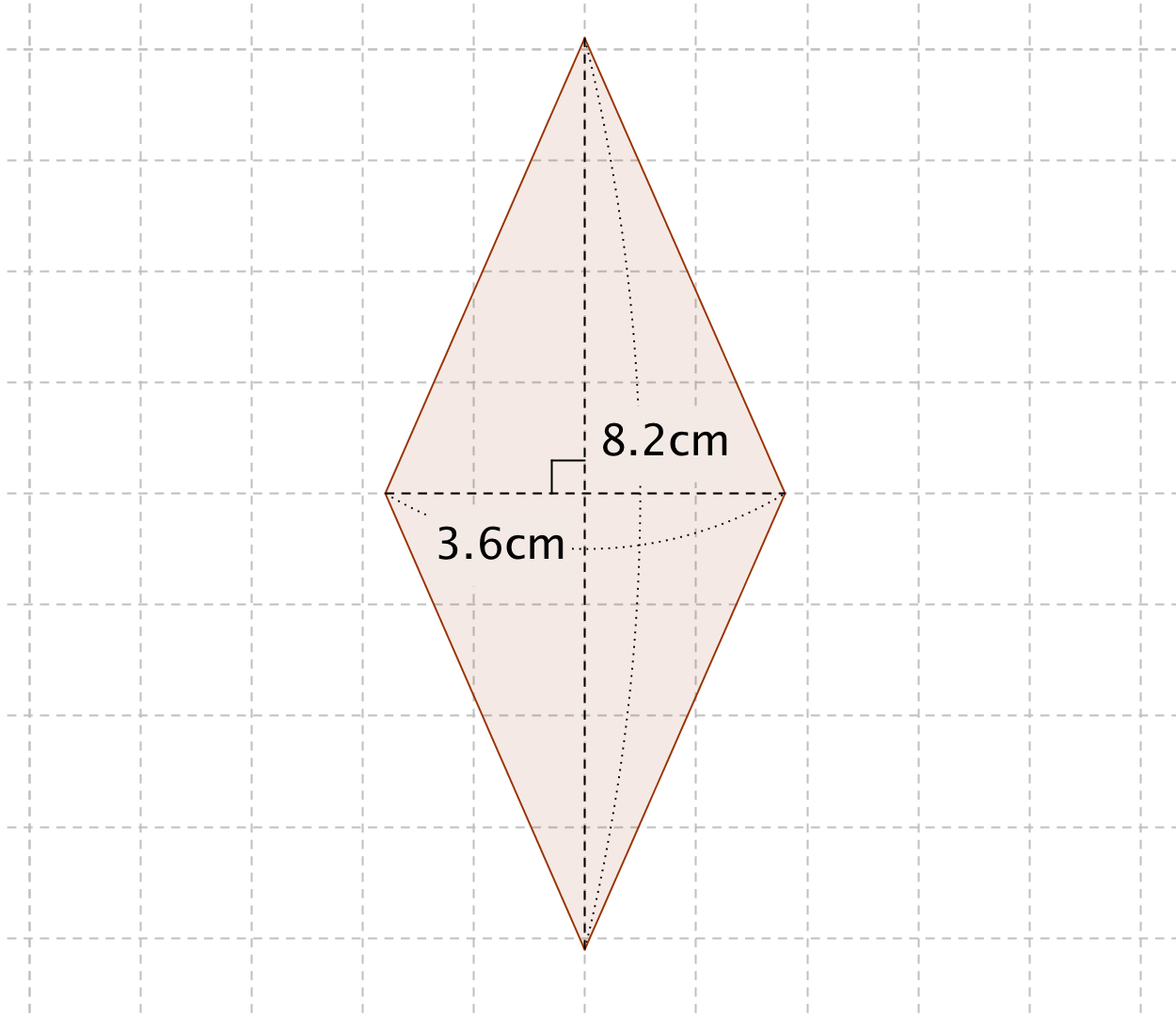
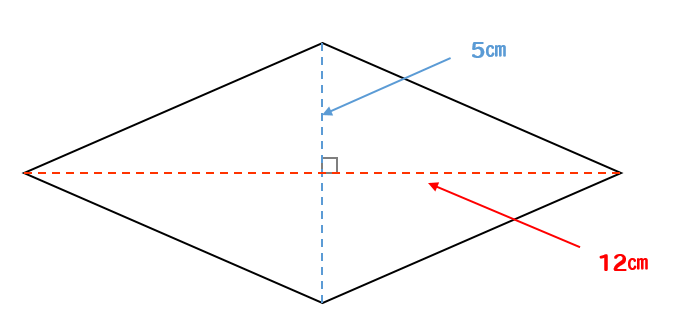
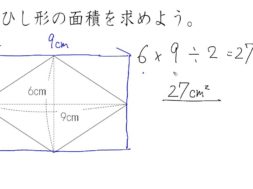
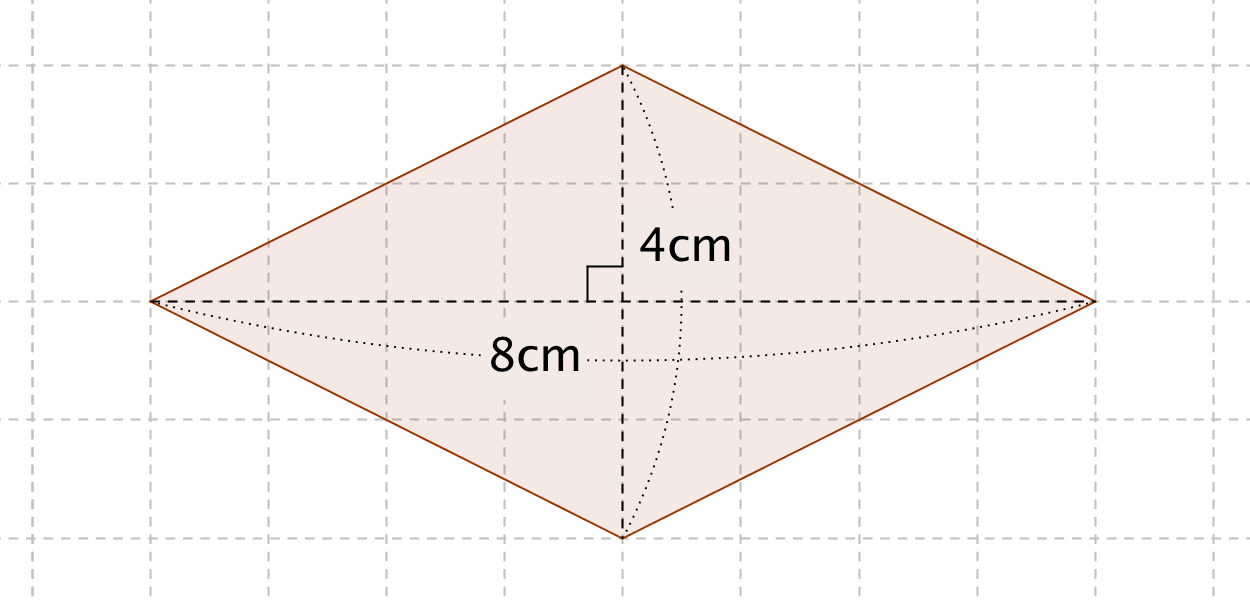
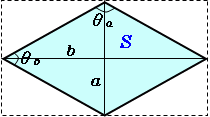
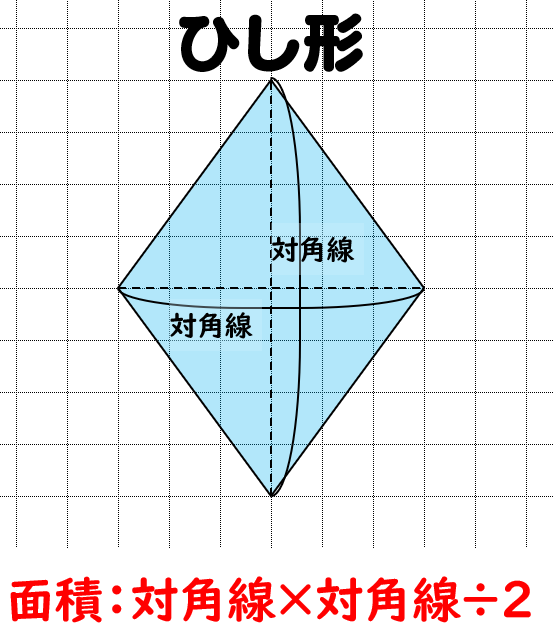
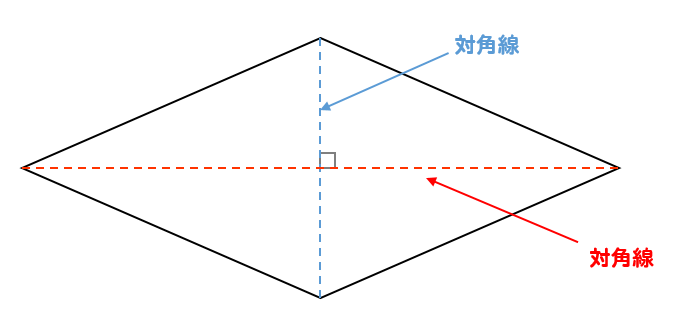
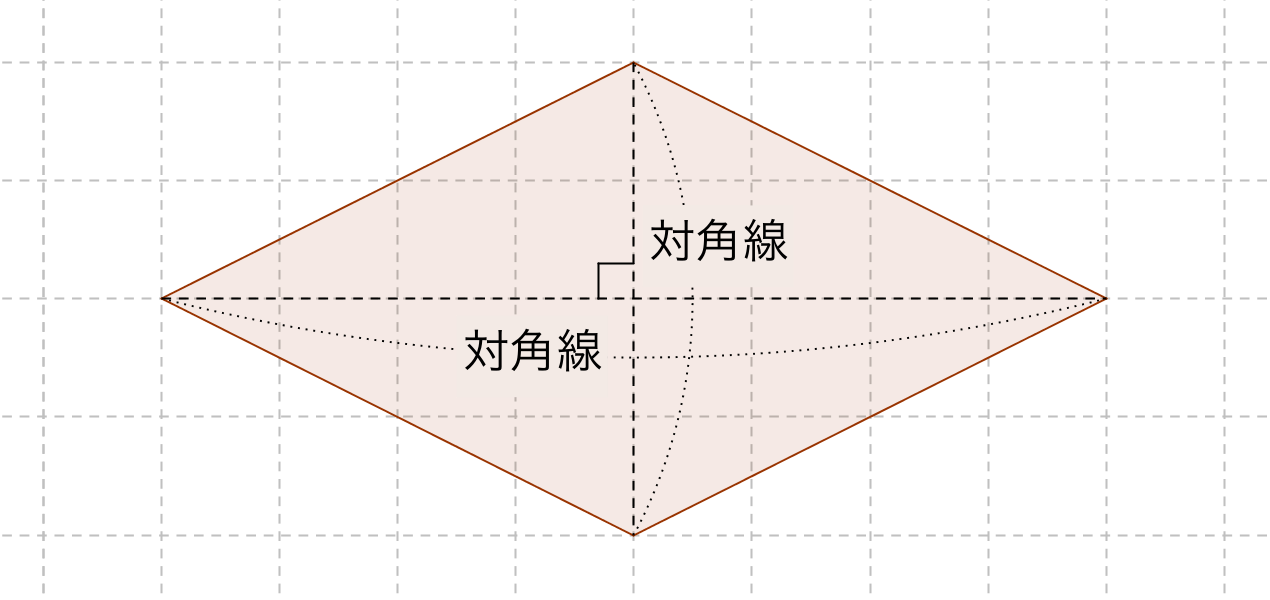
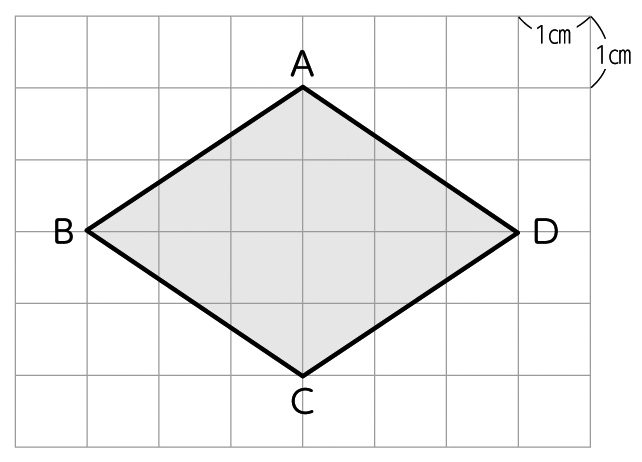
ひし形 の 体積 の 求め 方- たとえば、下の辺が4cm、上の辺が2 cm、高さ6cmの正四角錐台ABCDEFGHがあったとしよう。 この立体の体積は、 1/3 h ( a^2 ab b^2 ) = 1/3 × 6 × ( 4^2 4 × 2 2^2) = 2 × ( 16 8 4 ) = 56 cm^3 になるよ! めんどい計算式だけど、 落ち着いて計算してみよう!ひし形の面積 = 対角線 × 対角線 ÷ 2 それでは「ひし形の面積の公式」を使った「練習問題」を解いてみましょう。 「公式の考察」についても合わせてみていきます。 練習問題① 対角線が 8(cm)、4(cm)のひし形の面積を求めてください。 練習問題② 対角線が 36(cm)、(cm)のひし形の面積を求めてみましょう。 公式の考察
ひし形 の 体積 の 求め 方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  |  |
「ひし形 の 体積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「ひし形 の 体積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「ひし形 の 体積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「ひし形 の 体積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
 |  | |
「ひし形 の 体積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「ひし形 の 体積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「ひし形 の 体積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「ひし形 の 体積 の 求め 方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
半径 (はんけい) r の球の体積は、次の式で求められます。 球 (きゅう) の体積 \begin{align*} V = \frac{4}{3}\pi r^3 \end{align*} 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 (どうしゅつ) 方法と計算例は、「球の体積の求め方」をご覧ください。三角形の面積 ・正三角形の面積 1辺の長さを指定して、正三角形の面積を計算します。 ・三角形の面積(底辺と高さ) 底辺と高さから三角形の面積を計算します。 ・三角形の面積(2辺と間の角度) 2辺と間の角度から三角形の面積を計算します。





0 件のコメント:
コメントを投稿